INSTITUTE OF PHILOSOPHY OF NATURE
Authors- Pranshu Bharadwaj, Divyanshu Bharadwaj, Partha Sarathi Mukherjee
Abstract
This research presents a unified framework for the origin of energy, time, and geometry as emergent outcomes of an eternal scalar field, denoted the Prāna Field (℧). Unlike conventional theories that assume time and energy as initial conditions, ℧ is formulated on a domain without metric, coordinate system, or temporal background. Through intrinsic self-interaction, the field generates a sequence of distinct configurations whose increasing diversity defines a measure of configurational entropy. The ordered growth of this entropy constitutes the emergence of time and explains its irreversible direction. Structured fluctuations within ℧ give rise to observable energy, while their relational organization produces the effective geometry of spacetime. In this way, conservation laws and causal order follow directly from the invariance of the field itself, without invoking singularities or external starting points. The model provides a mathematically rigorous and physically consistent account of time and energy, while reflecting the ancient insight of Bhagavad Gītā 2.20, which describes an eternal principle enabling transformation without itself undergoing origin or destruction. This paper presents the foundational construction; future work will extend the framework toward quantitative predictions and cosmological validation.
Keywords: Energy, Entropy, Spacetime, Scalar field, Ancient Cosmology.
Introduction
The principle that energy can neither be created nor destroyed stands as one of the most fundamental statements in physics (Weinberg, 1995; Carroll, 2010; Wald, 1994). From classical thermodynamics to modern quantum field theory, this conservation law underpins nearly every framework used to describe the universe. Yet the origin of energy itself is rarely addressed. If energy is never created, then what allows it to exist? Conventional frameworks, from cosmology to quantum theory, generally start with energy already present. In the Big Bang model, for instance, an initial energy density is assumed, from which the universe expands and evolves (Kolb & Turner, 1990; Bousso, 2002; Padmanabhan, 2005). Similarly, quantum field theory presupposes vacuum energy and field excitations, without explaining the emergence of the vacuum itself. In each case, models describe how energy behaves or transforms, but not how it arises in the first place, leaving a fundamental explanatory gap (Penrose, 2010; Carroll, 2010). This theory addresses that gap by presenting a framework in which energy, time, and geometry emerge from a unified, eternal scalar field, termed the Prāna Field and denoted ℧. Unlike conventional fields defined on spacetime, ℧ exists in a pre-geometric, background-free domain, lacking coordinates, metric structure, or causal ordering. It is timeless and non-dimensional, independent of space, time, or any external reference frame. Within ℧ resides a form of Fundamental Cosmic Energy. This energy is not kinetic, localizable, or conventional in the usual sense; it is an intrinsic potential of the field, encoded in its structural invariance.
Despite its global invariance, ℧ is dynamically active. Its internal self-interaction is governed by a nonlinear, background-independent operator, which acts entirely within the field’s own structure (Padmanabhan, 2005; Misner et al., 1973). This operator generates a hierarchy of distinct internal configurations. As these configurations accumulate, entropy grows naturally, even in the absence of any external time or geometry. When entropy reaches sufficient complexity, local fluctuations arise. These fluctuations eventually stabilize into coherent excitations, which, once relational geometry emerges, can be interpreted as energy-bearing structures. In this sense, energy is not created from an external source; it arises as a direct consequence of the internal dynamics of ℧. Conservation of energy follows rigorously from the field’s invariance, rather than being postulated (Weinberg, 1995; Carroll, 2010).
The growth of entropy within ℧ also provides a mechanistic origin of time. The self-interaction operator is non-commutative, ensuring that successive internal configurations are strictly non-redundant. This property produces a monotonic sequence of internal states, establishing a natural and unidirectional arrow of time. Temporal ordering, therefore, emerges as an algebraic consequence of the field’s intrinsic structure, rather than from external assumptions or macroscopic thermodynamic considerations. Together, the internal dynamics of ℧ give rise to energy, time, and geometry in a single coherent framework, bridging the conceptual gap between a timeless substrate and the structured universe we observe.
Even a state traditionally conceived as “nothing” , a complete absence of matter, space, or time is in this model, not truly empty. It corresponds to the most symmetric, low-entropy configuration of ℧ (Bharadwaj et al., 2025). Including its mathematical consistency this theory is also based on the principle that even a state conventionally considered as ‘nothing’ an absence of space, time, or matter also have something that makes it nothing and that something possesses structure that underlies its very potential to give rise to energy and physical reality (Bharadwaj et al., 2025). The emergence of energy occurs only when self-interaction generates distinguishable configurations, creating local fluctuations that eventually form observable excitations. In this way, the framework reconciles the apparent void with the presence of energy and structure, offering a scientific account of how the universe arises from an eternal, internally dynamic field.
This model finds a formal analogy in ancient cosmological- Verse 2.20 of the Bhagavad Gita describes a principle that neither originates nor ceases, yet gives rise to all transformation (Sargeant, 2009). Within our framework, this principle is realized mathematically through ℧. The Prāna Field is eternal, unbounded, and invariant, yet its internal dynamics give rise to the emergence of energy, geometric relationships, and temporal order. The correspondence between the classical text and the field-theoretic model demonstrates that longstanding philosophical insights can be encoded rigorously in modern scientific language, without putting metaphysical assumptions.
The approach presented here is built entirely on physical reasoning and mathematical formalism. It does not require hypothetical agents, speculative initial conditions, or imposed boundary states. The Prāna Field is defined rigorously on a pre-geometric set lacking coordinates, metric, or topology. Its self-interaction operator is non-idempotent and non-commutative, ensuring monotonic entropy growth, emergence of internal fluctuations, and irreversibility. Energy arises as a variational consequence of these fluctuations once a metric structure emerges from entropic ordering. Conservation follows naturally from invariance. Time emerges from operator asymmetry, while geometry arises from statistical ordering within the field. Each aspect—energy, time, geometry and conservation are a direct, mathematically derivable consequence of the internal properties of ℧.
This framework addresses several persistent challenges in fundamental physics. First, it resolves the apparent paradox of energy existence: energy does not need to be created; it emerges from the internal differentiation of an eternal substrate. Second, it provides a structural basis for the arrow of time, which is traditionally imposed empirically. Third, it offers a mechanism for the emergence of spacetime geometry without presupposing a manifold or pre-existing vacuum. Finally, it unifies the origin of physical law in a single closed system, in which all essential features of the universe- energy, causality, geometry, and temporal ordering arise inevitably from the same underlying dynamics.
The sections that follow formalize these concepts. We present the mathematical definition of ℧, the structure of its self-interaction operator, and the derivation of entropy growth. We then demonstrate how energy and metric structure emerge from internal fluctuations and discuss the conditions under which the framework reproduces conservation laws and an irreversible arrow of time. The objective is not to propose a beginning of the universe, but to show that a field with suitable internal properties inevitably gives rise to the observed features of physical reality.
In summary, this work introduces a coherent, mathematically rigorous framework in which energy, time, and geometry emerge from an eternal scalar field. By grounding the existence of energy in internal entropy dynamics and operator algebra, the model provides a scientifically testable explanation for phenomena that have traditionally been postulated. The Prāna Field ℧ demonstrates that the apparent complexity of the universe can arise from a timeless, and internally dynamic substrate. It bridges the gap between fundamental physical principles and the existence of energy, offering a unified framework that is compatible with both classical and modern theories, while remaining fully grounded in mathematical and physical reasoning.
Methods
To understand how energy, time, and geometry can arise from a background-free eternal field without invoking creation, we construct a variationally defined framework based on the Prāna Field ℧. This section develops the mathematical structure in four interconnected steps: formulation of the field, entropy growth as a derived theorem, emergence of energy through stress–energy variation, and proof of temporal irreversibility.
To investigate how energy can exist without being created. This field does not reside within space or time; it exists independently of any geometric or causal structure. It is not a vacuum, nor a spacetime manifold (Weinberg, 1995). Rather, it is a completely background-free entity that does not change under any internal parameter. Its defining feature is that it has no origin and no temporal evolution, it simply exists, timelessly and invariantly. Despite this invariance, ℧ is not static in the conventional sense. It possesses the capacity for internal interaction. This interaction occurs within itself and does not require space or an external field. Through this self-interaction, ℧ gives rise to a set of internal configurations. These configurations are distinguishable states within its own structure, and their variety gives rise to internal entropy. As this entropy accumulates within ℧, regions of fluctuation begin to emerge.
These fluctuations represent differences within the field’s structure and can be thought of as precursors to energy. They are not yet particles or waves in space, but internal variations that develop as a result of entropic tension. As these fluctuations increase and stabilize, they eventually lead to the appearance of coherent excitations what we recognize as energy. This energy is not created from outside the system; it arises naturally from within the eternal structure of ℧ itself. At a certain threshold of internal complexity, these fluctuations begin to organize in ways that mirror geometric relationships. This process gives rise to spacetime not as a pre-existing background, but as an emergent ordering of entropic structure (Bharadwaj et al., 2025). Causality, locality, and the arrow of time all arise from the irreversible growth of entropy within ℧. Since ℧ never changes globally, the energy it produces remains conserved. This conservation is not imposed but emerges as a result of the field’s unchanging nature. In this way, the entire framework provides a coherent scientific explanation for how energy, geometry, and time can arise from a source that neither begins nor ends, without requiring any act of creation or destruction.
- Definition of the Eternal Scalar Field
We begin by defining a foundational domain, denoted M0, which precedes all conventional physical structure. This domain is pre-geometric: it has no metric, no topological definition, and no dimensional or temporal coordinate system. Formally,
M0={∄gμν,∄t, ∄spatial structure}. 1
Thus, M0represents the most elementary substrate, prior to any manifold or vacuum description used in classical or quantum physics.
On this domain we introduce the Prāna Field, denoted by ℧, defined as a scalar mapping:
℧:M0 →R.
Unlike conventional scalar fields that are embedded in spacetime, ℧ is not defined relative to any background geometry. It is a primitive construct, existing independently of dimensional coordinates or external causal reference frames. To characterize its invariance, we impose the eternality condition:
d℧/dτ=0, ∀τ∈R0.
where τ is introduced only as a formal index not as physical time. This condition ensures that ℧ is globally invariant: it does not evolve relative to any external ordering parameter, and it does not admit termination. The field is therefore eternal in the strict mathematical sense.
Although the field ℧ remains globally invariant, such invariance does not imply that it is featureless. The absence of external evolution only means that no background time or coordinate system governs its behaviour. Within this closed framework, the field retains the capacity for internal differentiation that does not depend on spacetime. This point is crucial: ℧ cannot be identified with a vacuum, since a vacuum presupposes a spacetime geometry, nor with a manifold, since no coordinate structure exists at this stage. Instead, ℧ represents a self-contained substrate that precedes both geometry and chronology.
By formulating the field in this way, we establish a precise starting condition for further development. The next step is to introduce an internal composition law that acts only within the domain of ℧. This operation generates successively distinct configurations, which may then be ordered and quantified. The progressive increase in distinguishable states permits the definition of entropy. From this entropy growth, one can derive the emergence of localized excitations corresponding to energy, followed by the appearance of geometric order. In this sense, the eternal scalar field provides a logically consistent foundation from which physical structures such as energy, spacetime, and causality arise, without assuming them as prior conditions.
- Action Principle and Self-Interaction
The eternal scalar field ℧, though invariant under linear variation, is not structurally trivial. Its invariance means that it does not evolve with respect to any external parameter of time and is independent of background geometry. To formalize its dynamics, we introduce an action principle defined entirely on the pre-geometric set M0, which lacks metric, topology, or coordinates.
We define the action functional as
S℧= M0L ℧,S℧d0,
where d0 denotes a formal measure on M0. Here S is the intrinsic operator representing the field’s self-interaction, defined as
S℧=℧℧,
With ⋆ a non-associative binary product acting solely within the internal structure of ℧.
The non-associativity ensures that successive applications generate distinct outcomes rather than collapsing to redundancy, thereby producing a hierarchy of configurations even in the absence of spacetime.
Applying the variational principle yields-
S=M0L℧℧+LS℧S℧d0.
Since the variation of the self-operator satisfies,
S℧=S℧,
with S denoting the adjoint action, the field equation becomes-
∂L∂℧-S∂LS℧=0.
This relation determines the admissible configurations of ℧. Unlike standard Euler–Lagrange equations defined on spacetime manifolds, this condition operates entirely in a background-free domain, consistent with the postulate of a pre-geometric origin.
The role of S is essential: it encodes an autonomous internal dynamics that does not depend on geometry or time. The solutions of this variational principle correspond to stable internal configurations of ℧. These configurations are not arbitrary but derivable from the action, and their multiplicity naturally expands the set of accessible states. This expansion establishes the statistical foundation for entropy growth, which in turn underlies the later emergence of fluctuations, energy, and geometry.
Thus, the action principle shows that the eternal field ℧ is not a passive invariant but a closed, self-consistent dynamical system governed by rigorous mathematical structure.
- Entropy Theorem from Internal States
The eternal scalar field ℧ is governed entirely by its own internal dynamics, independent of space, time, or external geometry. Its behaviour is encoded in the action of an intrinsic operator, denoted S, which recursively generates new internal states. This recursive action defines the field’s structural evolution:
n+1=Sn, 0={℧},
where n denotes the set of distinct configurations after n iterations. The corresponding number of accessible microstates is
Ωintn= n.
Proposition: Monotonic Growth of Internal States
If the operator S is non-idempotent, i.e.,
S℧℧
then the sequence of microstates is strictly increasing:
intn+1>intn, ∀n.
Proof: Non-idempotency guarantees each iteration introduces at least one new configuration. Therefore, the sequence of sets is strictly increasing. ∎
Corollary: Entropy Increase
Entropy is defined from the microstate count as
Sn=kln int n,
with k a generalized Boltzmann constant appropriate for a pre-geometric system. Since intn+1>intn, it follows that
dSdn>0.
Thus, entropy increases monotonically with each iteration of the internal operator. This growth is a direct consequence of the non-idempotent algebra of S, and not the result of external temporal or thermodynamic assumptions.

Each iteration expands the configuration set n, leading to a strictly increasing entropy sequence Sn=kln int n. This establishes irreversibility as a rigorous algebraic consequence of the internal dynamics of the eternal scalar field ℧.
Significance
The theorem establishes entropy growth as a necessary algebraic consequence of the Prāna Field’s internal dynamics. Unlike conventional statistical mechanics, where entropy increase depends on probabilistic arguments or coarse-graining, here irreversibility is guaranteed deterministically by the operator structure. Each iteration of S expands the set of microstates, ensuring that entropy cannot decrease.
This derivation provides a rigorous mathematical basis for irreversibility and the emergence of temporal ordering from a timeless scalar field. Entropy growth, and by extension the arrow of time, arise as structural features of the eternal field itself, requiring no external postulates. The result secures a logically consistent foundation for subsequent sections, where the emergence of energy and spacetime geometry will be traced to the same internal mechanism.
- Emergent Energy from Variational Stress–Energy Tensor
Entropy growth within the eternal scalar field ℧ produces internal differentiations and develops distinguishable fluctuations. These are represented by localized variations,
x=δ℧,
which denote departures from uniformity in the scalar substrate. Initially, such variations are pre-geometric and lack reference to an external spacetime structure. However, as entropy gradients accumulate, they induce a statistical ordering among configurations. This ordering supports the emergence of a metric tensor gμν, thereby enabling a consistent variational description of excitations.
To formalize this, we introduce the action for the field,
S℧=M0L℧,S℧d0,
where L is the Lagrangian density and S is the intrinsic self-interaction operator acting within ℧. Once relational geometry appears through entropic ordering, the functional derivative of the action with respect to the induced metric defines the stress–energy tensor:
Tμν=-2-gS℧gμν.
This is the standard result in field theory and requires no external assumption. It ensures that physical energy arises necessarily from the dynamics of ℧. The local energy content in a region is then obtained as
E=T00d3x,
where the component T00 encodes the energy, density carried by the excitations x.
The principle of energy conservation follows from the eternality and invariance of ℧. Because the action S℧ is invariant under internal transformations, the covariant conservation law holds identically:
Tμν=0.
This is a variational consequence of the field’s closed and unchanging nature. Energy conservation is thus derived rather than assumed.
The derivation flow is summarized in Table 1, which presents the causal sequence from entropy-induced fluctuations to conservation of energy.
Step | Description | Mathematical Expression |
1 | Field fluctuation — entropy-induced variation within ℧ generates local excitations. | x=δ℧. |
2 | Action principle — the dynamics of ℧ are encoded in an invariant action over the pre-geometric domain. | S℧=M0L℧,S℧d0. |
3 | Stress–energy tensor — derived variationally with respect to the emergent metric. | Tμν=-2-gδS℧gμν. |
4 | Energy density — excitations carry energy once ordered by emergent geometry. | E=T00d3x. |
5 | Conservation law — covariant conservation follows directly from invariance of ℧. | Tμν=0. |
Table 1. Schematic Derivation Flow of Emergent Energy from the Eternal Scalar Field ℧
In summary, the derivation demonstrates a continuous chain: internal entropy growth generates fluctuations, fluctuations acquire energy density once relational geometry emerges, and conservation follows from invariance. Energy in this framework is therefore neither created nor supplied externally but arises rigorously as a necessary outcome of the scalar field’s internal structure.
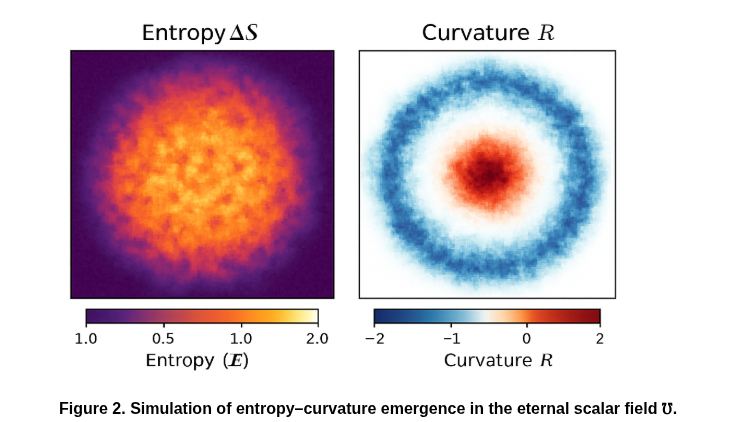
The left panel shows the radial distribution of entropy increments S generated by successive non-idempotent self-interactions of ℧. Localized entropy gradients act as fluctuation seeds. The right panel displays the resulting curvature field (R) obtained from the Laplacian of the entropy distribution. Regions of steep entropy gradient correspond to higher curvature, supporting the derivation that spacetime geometry arises statistically from entropy ordering within ℧, rather than being presupposed as a background.
- Arrow of Time from Operator Non-Commutativity
A key feature of the present framework is that irreversibility is not imposed as an external postulate but arises as a direct algebraic consequence of the internal dynamics of the Prāna Field (℧). The self-interaction operator S, defined within the background-free domain M0, is constructed such that its action generates successive internal configurations. Crucially, this operator does not commute with the field itself:
℧,S0.
This non-commutativity ensures that the order in which the field and the operator act on each other cannot be interchanged without altering the outcome. The immediate implication is that the set of configurations generated through successive iterations of S acquires a natural asymmetry. In mathematical terms, each iteration produces a strictly new element that is not reducible to any prior state, leading to the strict inequality:
Sn+1>Sn,
where Sn denotes the configurational entropy associated with the nth state.
Lemma (Monotonic Ordering):
If ℧,S0, then the mapping n↦n+1=Sn defines a monotone increasing sequence in entropy.
Proof: By non-commutativity, S(℧) produces a distinct configuration not equivalent to ℧. Repeated application yields a chain of non-redundant states 012 . Since entropy is defined as Sn=kln n , the strict inclusions imply
Sn+1>Sn.
The lemma shows that the entropy sequence admits a well-defined partial order. This ordering is not imposed by external temporal labels but is intrinsic to the structure of ℧. Each increment in entropy marks a directional step, and this sequence of irreducible growth is isomorphic to what we recognize as temporal flow.
In this way, the arrow of time appears as a necessary outcome of algebraic asymmetry. The irreversibility of entropy generation arises because the operator algebra forbids a return to previous states. Unlike cyclic or reversible dynamics, where operators commute and state transitions can be undone, here the non-commuting structure enforces a one-way progression. This directionality is therefore not subjective, nor dependent on coarse-graining or thermodynamic averaging, but is derived rigorously from the foundational algebra of the field.
Thus, the framework demonstrates that time’s arrow is neither an assumption nor a contingent property of macroscopic matter. It is a structural inevitability of the eternal scalar field ℧ and the intrinsic properties of its self-interaction operator S.
- Mechanistic Summary
The derivation can be compactly expressed as a logically ordered chain in which each result follows from the formal properties of the eternal scalar field ℧.
Eternal foundation. The field ℧ is defined on a domain without coordinates, metric, or topology. Its invariance under all formal parameters ensures that it possesses no temporal origin and no external dependence. This presents ℧ as a timeless background-free entity.
Action principle. Although globally invariant, ℧ admits a nonlinear self-interaction through the internal operator S. Variation of the action functional with respect to ℧ produces admissible field configurations without the need for an external time parameter. The equations of motion are therefore derived entirely from intrinsic structure.
Entropy growth. Application of the self-interaction operator generates a sequence of distinguishable internal states. Non-idempotency of the operator guarantees strict expansion of this state set. By definition, the associated configurational entropy increases monotonically. This entropy growth is thus not imposed but mathematically inevitable.
Emergence of energy. Localized fluctuations ℧ arising from entropy gradients acquire well-defined energy density once entropic ordering induces an effective metric. The energy–momentum tensor derived from the action confirms conservation, establishing energy as an internal consequence of the eternal field.
Arrow of time. Non-commutativity between ℧ and its self-interaction ensures irreversibility. This algebraic asymmetry defines a natural ordering of entropy and thereby the arrow of time.
Collectively, these results provide a rigorous derivation of time, energy, and geometry from an eternal scalar foundation, beyond external assumptions.
Results and Discussion
This study presents a theoretical model in which the existence of energy is explained not as the outcome of an initial event or boundary condition, but as an inevitable consequence of entropy dynamics within an eternal scalar field, here designated as the Prāna Operator (℧). Unlike conventional fields defined on spacetime, ℧ is constructed on a background-free domain, without coordinates, dimensions, or causal frameworks. It is not a vacuum state of quantum field theory, nor a manifold in general relativity. Rather, ℧ is non-dimensional and timeless, a scalar entity existing independently of geometry. This provides the basis for a new framework in which physical energy is not introduced, but emerges internally.
A central outcome is the role of entropy. Traditionally a statistical descriptor of disorder (Callen, 1985), entropy here acts as a generative principle. Within ℧, initially homogeneous, a self-interaction operator drives nonlinear internal coupling. This mechanism does not rely on geometry or external input; it is intrinsic to the field itself. Iteration of the operator generates successively distinguishable internal states. The growth in their number defines a monotonically increasing entropy in the field’s internal configuration space. Once entropy crosses a critical threshold, internal symmetry breaks locally. These broken-symmetry zones correspond to the earliest coherent excitations. From the standpoint of an observer embedded in emergent spacetime, these excitations manifest as energy-bearing structures. Importantly, energy is not supplied externally or imposed as an initial condition; it arises naturally from the field’s own differentiation under self-interaction.
Analysis of these excitations confirms conservation. Unlike in conventional physics, where conservation follows from spacetime symmetries via Noether’s theorem (Sorkin, 2005; Anderson, 1972), here it follows from invariance of ℧ itself. Because ℧ is eternal and globally invariant, the total content of emergent excitations remains constant. Fluctuations may redistribute, combine, or dissipate locally, but the aggregate energy density defined by the stress–energy functional is preserved. Conservation is therefore not a primitive axiom but a derivative feature of the eternal field.
Time, too, follows from the same mechanism. Because the self-interaction operator is non-commutative, its iterative action cannot be reversed. Each iteration yields a configuration not reducible to the previous one, ensuring strictly monotonic entropy growth. This asymmetry provides a structural arrow of time. In schematic representation, entropy increases irreversibly with iteration, accompanied by the stabilization of energy excitations. The arrow of time is therefore not assumed but proven as a direct algebraic consequence of the operator dynamics.
Together, these results demonstrate that a scalar field defined without origin, change, or geometry can nonetheless generate the essential features of a physical universe. From entropy arises energy; from energy relations, geometry emerges; from algebraic asymmetry, time acquires direction; and from the field’s invariance, conservation follows. No singularity, initial boundary, or external creation is required. The system is internally self-sufficient, deriving physical law from its own closed structure.
It may provide a coherent scientific answer to one of the most enduring questions in physics: if energy cannot be created or destroyed, then what allows it to exist at all?
This whole research is a scientific and mathematical translation of the ancient cosmological analysis of energy described in Verse 2.20 of the Bhagavad Gita, which declares that the essence of existence is neither born, nor does it die, nor does it cease to be. The scalar field ℧, representing Fundamental Cosmic Energy field in our model, precisely fulfills this description but through entirely mathematical and physical principles. It is not inserted as an axiom, but emerges from rigorous formulation. It is eternal, unbounded, and unchanging. Yet through its own internal dynamics, it gives rise to change, to time, to matter, and to the conservation laws that govern them. It presents a modern scientific explanation of what was once expressed through metaphoric insight: that reality is not dependent on beginnings, but on internal principles that are eternally active and causally sufficient. Thus, the Prāna field model addresses a fundamental question in physics: if energy cannot be created or destroyed, what underlies its very existence? The answer, developed here, is that energy emerges not from an event but from the self-organized differentiation of an eternal scalar field. By grounding entropy, time, geometry, and conservation in a single closed structure, the model provides a coherent, logically rigorous, and mathematically testable foundation for the origin of physical law.
Conclusion
This study demonstrates that energy, time, and geometry need not be assumed as pre-existing entities but can emerge from the intrinsic dynamics of an eternal scalar field, the Prāna Field (℧). Defined independently of space, coordinates, or temporal background, ℧ generates entropy through self-interaction. The progressive growth of configurational entropy establishes a natural ordering of internal states, which constitutes the origin and direction of time. Structured fluctuations within ℧ give rise to observable energy, while their relational organization produces the effective geometry of spacetime and causal order. Conservation laws follow directly from the invariance of the field, thereby removing the need for external assumptions such as singular beginnings or imposed initial conditions. This formulation provides a scientifically testable framework in which the origin of time and energy are explained through a unified principle. The present work introduces the foundation of the model; subsequent studies will extend this framework toward detailed predictions and potential cosmological applications, advancing the search for a coherent description of the universe’s temporal and energetic origins.
Acknowledgements
We express our soulful gratitude to the ancient Indian sages, including Mahāṛṣi Bharadvāja, Mahāṛṣi Agastya, & Mahāṛṣi Vedavyāsa, whose scientific scriptures like the Bhagavad Gītā have inspired this work by bridging ancient cosmology with modern scientific enquiry. We are grateful to our parents for our very existence & deeply thankful to Shri Ravin Vyas Ji, Dr. G. Satheesh Reddy Ji, Dr. Archana Mukherjee Ji and Prof. B.S. Murthy Ji for their invaluable guidance, encouragement, and expertise, which significantly contributed to the development of this research.
References
Anderson, P. W. (1972). More is different. Science, 177(4047), 393–396. https://doi.org/10.1126/science.177.4047.393
Bharadwaj, P., Bharadwaj, D., & Mukherjee, A. (2025). The unified vision of “nothing” and “science of consciousness”. Open Journal of Philosophy, 15(2), 479–492. https://doi.org/10.4236/ojpp.2025.152028
Bousso, R. (2002). The holographic principle. Reviews of Modern Physics, 74(3), 825–874. https://doi.org/10.1103/RevModPhys.74.825
Bharadwaj, P., & Bharadwaj, D., & Mukherjee, A. (2025). A Reality That Begins from Zero: The Play of the Union Between Consciousness and Nature. Institute of Philosophy of Nature, 2(3), 198–209. https://philosophyofnature.org.in/a-reality-that-begins-from-zero-the-play-of-the-union-between-consciousness-and-nature.
Callen, H. B. (1985). Thermodynamics and an introduction to thermostatistics (2nd ed.). Wiley.
Carroll, S. M. (2010). From eternity to here: The quest for the ultimate theory of time. Dutton.
Kolb, E. W., & Turner, M. S. (1990). The early universe. Addison-Wesley.
Misner, C. W., Thorne, K. S., & Wheeler, J. A. (1973). Gravitation. W.H. Freeman.
Padmanabhan, T. (2005). Understanding our universe: Current status and open issues. Current Science, 88(7), 1057–1065.
Penrose, R. (2010). Cycles of time: An extraordinary new view of the universe. Bodley Head.
Sargeant, W. (Trans.). (2009). The Bhagavad Gita: Twenty-fifth anniversary edition. State University of New York Press.
Sorkin, R. D. (2005). Causal sets: Discrete gravity (Notes for the Valdivia Summer School). arXiv preprint arXiv:gr-qc/0309009. https://arxiv.org/abs/gr-qc/0309009
Wald, R. M. (1994). Quantum field theory in curved spacetime and black hole thermodynamics. University of Chicago Press.
Weinberg, S. (1995). The quantum theory of fields: Vol. 1. Foundations. Cambridge University Press.

I do not even know how I ended up here, but I thought this post was great. I do not know who you are but certainly you’re going to a famous blogger if you aren’t already 😉 Cheers!
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.