INSTITUTE OF PHILOSOPHY OF NATURE
Abstract
The planets make different motions due to interaction with the sun and satellites make different motions due to interaction with their planet. Therefore, the motions of planets are required to be expressed relative to the sun and the motions of satellites are required to be expressed relative to their planet for working out their dynamics. Minute observation of orbital distances of planets and satellites reveals the unnoticed orderly placement of planets and satellites in geometrical progression against the old concept of continuous orbit for the solar system. Lack of perception of proper dynamics of the oscillation of the axis of the earth with respect to the axis of the sun has made it convenient to express the orientation of the North Pole end of the axis towards Polaris, a distant star. The sun being the main interacting body for planets, the oscillation of the axis of the earth relative to the sun is the cause oriented therefore relevant for the sun-based dynamics. Further, many dynamic parameters of planets and satellites exhibiting common features and phenomena are not given due attention. Observation shows that, the orbital planes of planets are close to equatorial plane of the sun; the inclination of axes of planets with the normal to the equatorial plane of the sun are acute angles except for retrograde planets whose angles are obtuse angles; the outer satellites of Jupiter and Saturn exhibit retrograde revolution; almost all orbital bodies rotate and revolve in the same direction as the direction of rotation of the central body baring a few. The major axes of elliptical orbits of all planets are oriented towards one direction and the major axes of elliptical orbits of all satellites of any planet are oriented towards one direction. Some of these phenomena are not given due importance.
The dynamics of prograde motion of orbital bodies cannot justify the retrograde motion of orbital bodies. This may bread doubt on the very characterisation of retrograde motion. This author scrutinized the parameters of retrograde orbital bodies and identified the error in characterisation of the North Poles of retrograde orbital bodies. If the south pole of a planet/satellite is erroneously characterized as North Pole then the prevailing prograde motion of the orbital body would be erroneously recorded as retrograde motion. The paper gives emphasis on the discrete nature of orbit in the solar system and also discusses present erroneous characterization of some motions of planets and satellites.
Key Words: – Planetary motion, Trajectory motion, Celestial bodies, Planet and Satellites
Introduction
We make different models of structure and functional mechanisms for systems in the unseen micro domain in the light of known structure and functional mechanisms perceived in the macro domain to understand the functioning of nature in the micro domain and their interaction on systems of the macro domain. If our understanding of the structure of the solar system is incomplete and defective then developing the planetary atomic model would also be defective and the model is likely to fail in justifying the structural stability and the spectral features of the atom.
The rotation of the sun makes its axis of rotation, direction of rotation, North Pole, South Pole, equator and equatorial plane. These parameters of the sun become the reference for characterizing the orbital and rotational parameters of planets of the sun. Such characterization is relevant for the gravity-based dynamics of the sun-planet system. Planet also rotates and forms its axis of rotation, direction of rotation, North Pole, South Pole, equator and equatorial plane. The revolution of a planet forms the axis of revolution, direction of revolution, north and south poles on the sphere of revolution and its orbital plane. These parameters of planets are required to be characterized relative to the sun for the purpose of dynamics because the sun is the main interactive body for the planets. Similarly, the orbital parameters of satellites are required to be characterized relative to their planet. We can specify the inclination of the orbital planes of planets with reference to the equatorial plane of the sun; the direction of rotation and revolution of planets with reference to the direction of rotation of the sun. These types of characterization of the motions of planets are relevant to the dynamics of interacting bodies. The dynamic parameters of a planet can as well be described relative to any non-interacting distant star but such a relative motion does not help in working out the dynamics of planets. The early concept (geocentric concept) was that the sun goes around the earth. This relative motion is not useful for the dynamics. The planets that go around the sun were discovered subsequently which helped in developing the gravity-based dynamics of the solar system. The orientation of the North Pole end of the axis of the earth is described with reference to Polaris, the distant star. There is nothing wrong in such relative characterization from an observation point of view but it is less important for the dynamics of the axis of the earth. We cannot find an answer as to why the North Pole end of the axis of the earth points towards Polaris? On the other hand, if the motion of the axis of the earth is described relative to the sun, then it would be found to oscillate with respect to the axis of the sun where the north and south poles of the earth alternately come nearer to the sun. The mean position of the axis of the earth is normal to the equatorial plane of the sun. The new characterization has scope of understanding why the mean position of the axis of earth is normal to the equatorial plane of the sun? And why does the axis of the earth oscillate about its mean position with reference to the axis of the sun? The dynamics of oscillation of the axis of the earth is discussed in a separate article in this issue of the journal. The dynamic parameters of planets and satellites have some common features and phenomena which have not drawn due attention. For example, the orbital planes of planets are close to equatorial plane of the sun; the inclination of axes of planets are acute angles except for the retrograde planets whose inclinations are obtuse angles; the outer satellites of Jupiter and Saturn exhibit retrograde revolution; almost all orbital bodies rotate and revolve in the same direction as the rotation of the central body baring a few. The major axes of elliptical orbits of all planets are oriented towards one direction and the major axes of all satellites of any planet are oriented towards one direction. According to this author, each of the exhibited phenomena has a definite cause which is answerable from dynamics. The dynamics of orbital bodies in prograde motion has limitations in explaining the retrograde motion which leads one to doubt on the very characterization of retrograde motion. In this regard this author identified the error in characterizing the North Poles of retrograde orbital bodies. If the south pole of a planet/satellite is erroneously characterized as North Pole then the actual prograde motion of the planet/satellite would appear as if having retrograde motion. This has happened in our characterization of retrograde rotation and revolution of planets and satellites though in reality, they have only prograde motion. All planets and satellites rotate and revolve in prograde i.e. same direction as the direction of rotation of their central body.
The orbital bodies of a central gravitating body exhibit a definite pattern of their orbital distances [1] showing discrete nature of orbit in the solar system. The orbital bodies also exhibit similarity in most of their orbital parameters. Some of these phenomena are simply noted without serious analysis. At present celestial dynamics of the solar system is confined to Kepler’s observation of planetary motion. This author feels it is required to justify the following features and phenomena of orbital bodies through appropriate dynamics.
- Why the orbital bodies in the solar system (planets and satellites) have orderly placement (in G.P. series) revealing the discrete nature of orbit in the solar system similar to that in the atomic system?
- Why does Mercury, Venus and all satellites don’t have any orbital bodies?
- What is the torque transfer link between the orbital body and the central body that ensures conservation of angular momentum of an orbital body? How exactly does the centripetal acceleration of an orbital body due to gravity increase the tangential velocity in conservation of angular momentum?
- The rotational motion and the orbital motion don’t have any bearing, so why do satellites have one rotation per revolution?
- Why do most of the orbital bodies revolve and rotate in the same direction as that of the central body?
- Why are the axes of orbital bodies near-perpendicular to equatorial planes of their central body?
- Why does the North Pole end of the axis of the Earth point towards Polaris?
- Why are the orbital planes near-parallel to the equatorial plane of a central body?
- The interplanetary space as conceptualised by Newton is free-space (relational space). Thus, the motions of orbital bodies do not experience any resistance to motion from the free space medium. Space is no more relational but physical, which is capable of rendering high frequency wave motion and guiding the motions of celestial bodies in the space-time curvature. One may wonder, why the physical space doesn’t offer any resistance to different motions of celestial bodies. If physical space offers resistance during motion of orbital bodies then there is an absolute need of a motive force that overcomes the resistance offered by the physical space.
- Why do the major axes of elliptical orbits of all planets orient towards one direction and the major axes of all satellites of a planet orient towards one direction?
The Present dynamics of celestial bodies need to be augmented for justifying the above phenomena. For the purpose of dynamics of planets in the solar system, the parameters of planets are required to be characterised relative to the Sun. Likewise, the dynamic parameters of satellites (moons) are required to be characterised relative to their planet. Thus, the inclination of orbital planes of planets are required to be characterised relative to the equatorial plane of the sun and the inclination of the orbital planes of the satellites are required to be characterised with reference to the equatorial plane of their planet. Similarly, the inclination of the axes of the planets are required to be characterised with respect to the axis of the sun and the inclination of the axes of the satellites are required to be characterised with respect to the axis of their planet. The above characterisation of orbital bodies is important for working out the dynamics of orbital motion, dynamics of inclinations of orbital planes and dynamics of inclination of axes etc.
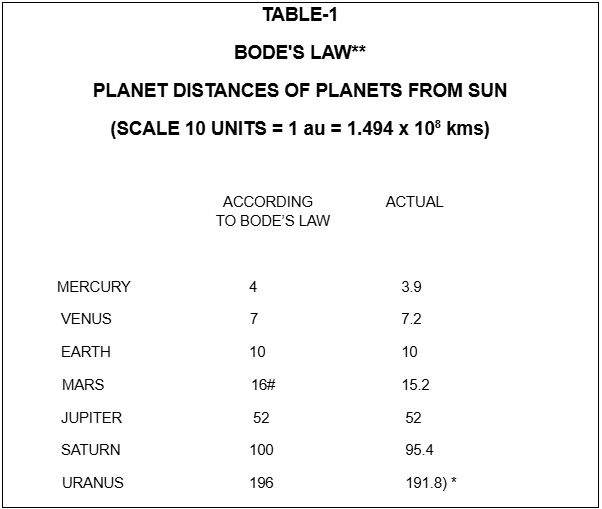
Discrete Orbit in Planetary System
Examination of orbital distances of planets revels discrete nature of orbit in the solar system. Titus and Bode first proposed a correlation among the distances of planets known then which subsequently became known as Bode’s law. The law states: Take numbers 0, 3, 6, 12, 24, 48, 96 and 192 each of which apart from the first is double its predecessor. Now add 4 to each giving 4, 7, 10, 16, 28, 52, 100 and 196. Taking the earth’s distance from the sun as 10, these figures give the distances of the remaining planets with remarkable accuracy as shown in Table-1. When Uranus was discovered it fitted well into Bode’s scheme, thus Bode’s law was verified successfully. Further Bode’s law was productive in discovering the asteroid belt in the gap between Mars and Jupiter. However, Bode’s law doesn’t work for Neptune and Pluto and satellites of planets for which astronomers discarded Bode’s law. According to this author, a verified and productive law cannot be rejected even if it has some limitations. Bode’s law has the scope of identifying the discrete nature of orbit in the solar system which has a great value in discovering harmony between the atomic system and solar system. In view of the above, a serious attempt is required to be made in overcoming the limitations of the Bode’s law. In this regard, this author has developed a new mathematical correlation [1] which overcomes the limitations of Bode’s law.
Bode’s Law can be written in the following mathematical form.
Dn = (4+3 x 2n)/10 (1.1)
Where, Dn is the distance of the nth orbit from the sun (except for the mercury) in astronomical units (AU)
n is an integer and can have values 0,1,2,3 ……….
We may generalize the expression by writing
Dn = (a + b cn)k
Where, a, b, c are constants of the central gravitating body
K is the scale constant
ak is the distance of the mercury from the sun
The equation 1.1 can be written in the modified form as:
D’n = z x 2n (1.2)
Where,
D’n is the distance of nth principal orbit of the central gravitating body measured from any (conventionally innermost) principal orbit/shell as the reference.
z is the nucleus constant of the central gravitating body.
n is an integer, having values 0, 1, 2, 3 ….
* (The asteroids, Uranus, Neptune and Pluto were not known during the time of Bode). ** Values taken from the book ‘Astronomy’ by Patrick Moore, Old bourne, LONDON, 1964.
# Maximum percentage of error = 16-15.215.2 ×100=5.263%
The satellites of Jupiter also having outwardly expanding order of placement is quite tempting for finding out a GP series correlating the placement of satellites. Here, it is seen that a considerable number of satellites do respond well for their placement correlating through a GP series while the others deviate considerably. One might ask a serious question – why after all a group of planets and satellites respond to GP series for their placement? The response is so striking that it just cannot be ignored for being a coincidence. At this juncture, the locations of the satellites of the Jupiter and the Uranus, those exhibiting different norms (those having a misfit in the GP series) may be examined in detail for finding some clue. It is noticed that some of the above satellites exhibit a tendency of forming closer groups around certain orbits. Referring to Fig. 1, it may be seen that, around a distance of 1.18 x 107 km from Jupiter, the satellites form a grouping with closer intervals. In the similar manner around a distance of 0.646 x 105 km from the Uranus, the satellites of the Uranus also form similar grouping.
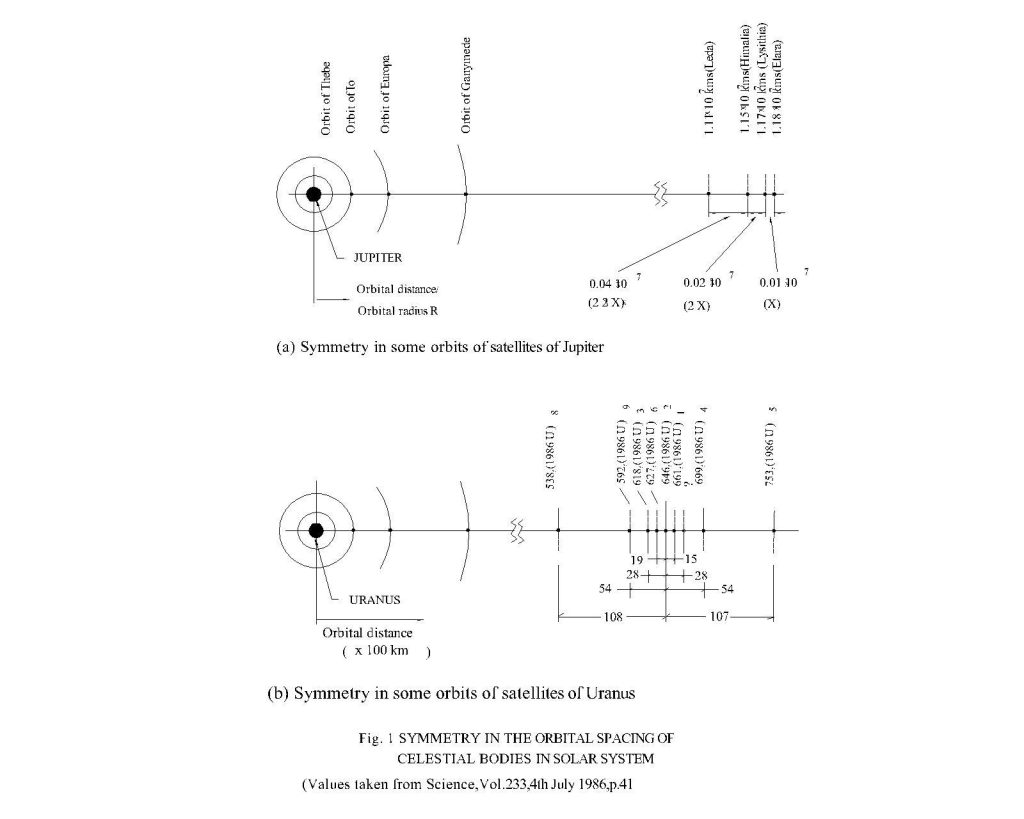
The orderly spacing of the satellites those don’t respond to the locations conforming to the GP series originating from the planet are as if they were placed in another GP series originating from a principal orbit. These placement sites may be called as sub-orbits of the principal orbit.
In the light of the new concept of sub-orbits of a principal orbit, a new model for correlating the distances of orbital bodies is proposed by the author in Fig.2. This new thinking goes in coherence with the existence of many orbital associating an orbit in the atomic system.
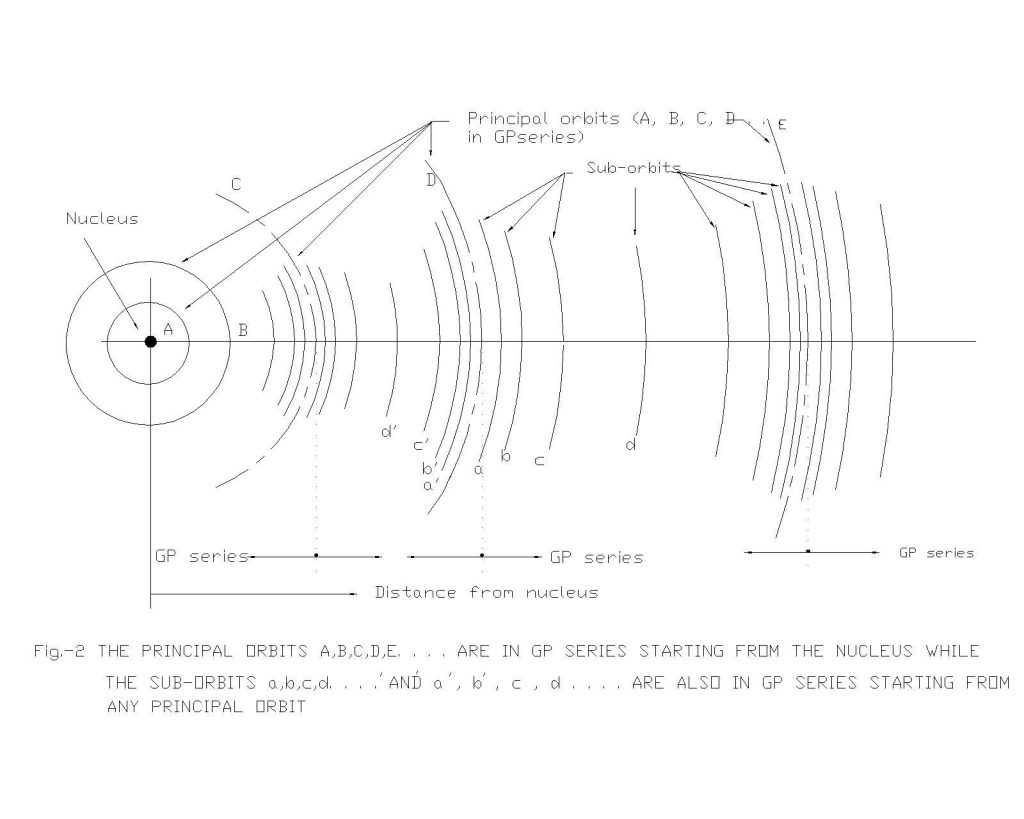
The placement of all orbital celestial bodies (Planets and satellites) of the solar system is now found to be discrete instead of the age-old concept of continuous orbit. The new consideration of principal orbit and the sub orbits of principal orbit conforming to GP series establishes the location of orbital bodies (Planets and satellites) which conforms to actual location of celestial bodies [1]. The new correlation of orbital distances matches with observed orbital distances with remarkable accuracy.
Sun-based characterisation of the fixed inclination of axis of the earth and other planets
At present the north-pole-end of the axis of earth is characterized as inclined towards Polaris, the distant star, and the axis further makes a cone of precession. There is nothing wrong in this relative characterization of the axis of the earth. However, we do not find any preferential attraction from Polaris to the North Pole of the earth. On the other hand, the earth derives its motive forces from the sun for all kinds of motion. Therefore, we need to characterize the motion of the axis of the earth relative to the axis of the sun. While doing so it is found that the axis of the earth makes an angular oscillation relative to the axis of the sun from its mean position which is normal to the equatorial plane of the sun. This is clear from the fact that the north-pole and the south-pole of the earth alternatively come nearer to the sun. In addition to this axial oscillation, the earth revolves around the sun and the period of revolution matches with the period of oscillation of the axis. The observed fixed inclination of the axis of the earth is the resultant of orbital motion and the oscillation of the axis with respect to the axis of the sun. Similarly, the fixed inclination of the axes of other planets can be justified from oscillation of their axes with respect to the axis of the sun and their orbital motion.
The satellites of any planet also have fixed axial tilts which imply the axes of satellites also oscillate with respect to the axis of their planet and the period of oscillation matches with their period of revolution. The mean position of the axis of a satellite is normal to the equatorial plane of its planet about which the axis oscillates in the direction of the planet.
The new mass-space interactions as the cause of gravity [2] and new non-electric charge interactions of celestial bodies [3] have scope of explaining the dynamics of the axis of the earth.
Elliptical orbit of planet and satellites with common directional orientation
Kepler made observation on the orbital motions of planets and stated
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet’s orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
These statements are known as Kepler’s Laws. Kepler’s laws are purely observational. Newton developed the gravitation-based dynamics to explain the Kepler’s laws of planetary motion. Kepler missed the vital point in his observation that the elliptical orbits of planets are close to circle having small eccentricity. It is, as if, the stable orbit is circular that undergoes minor directional deformation due to the external (galactic) field effect which is common to all planets. This new concept not only explains why the orbits of planets are elliptical and the elliptical orbits are close to circle but also explains why the major axes of the elliptical orbits of planets are oriented towards one direction (Fig.3). This phenomenon remains valid for the orbits of satellites where the external field is produced by the sun. This author has discussed the dynamics of elliptical orbit of planets and satellites and their unidirectional orientation in another paper in this issue of the journal.
Error in characterisation in North Pole of poles Venus, Uranus and Pluto leading to misconception of retrograde rotation of planets
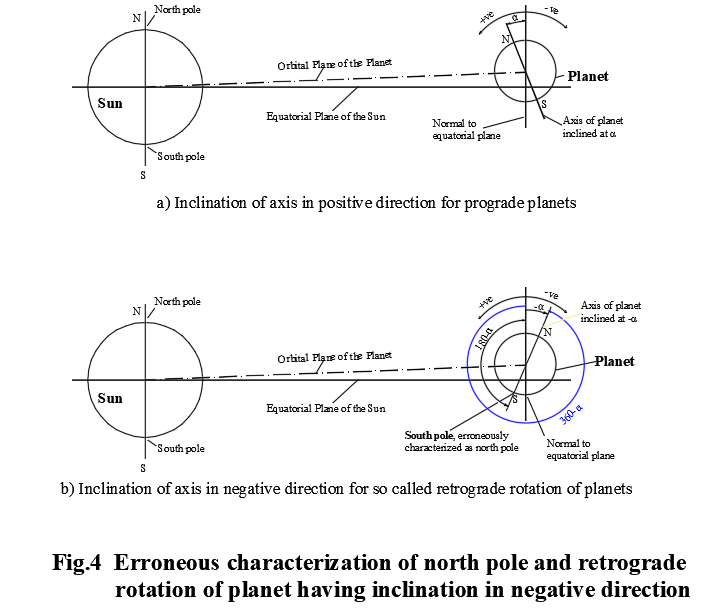
The direction of rotation of any planet is characterised by conventionally viewing from its North Pole end. Most planets rotate anticlockwise with reference to the North Pole. However, the planet Venus, Uranus and Pluto are observed to have clockwise rotation from their North Pole. Any planet observed rotating anticlockwise with reference to the North Pole shows clockwise rotation with reference to the South Pole.
The author has explained the cause of rotation of an orbital body by considering the new fluid dynamics model of the solar system. Following the fluid dynamics model, the directions of rotation of all planets have to remain the same as the direction of rotation of the sun. The retrograde rotation of Venus, Uranus and Pluto is a violation to the above fluid dynamics theory. The author anticipates error in the characterisation of the North Pole of these planets. If somehow the south pole of a planet is erroneously characterised as North Pole then the observed direction of rotation of the planet would be reversed (retrograde). One may wonder as to how such a major mistake persists even today when astronomy has advanced a lot! In view of the above, the author reviewed the definition of North Pole set by the International Astronomical Union (IAU). He found the flaw in the definition for characterization of the North Pole of a planet. The International Astronomical Union (IAU) defines a planet’s North Pole as the pole that’s in the same celestial hemisphere as Earth’s North Pole, relative to the solar system’s invariable plane. This definition is not foolproof because a planet remaining in the same celestial hemisphere as earth’s North Pole can have both poles in the same hemisphere. Only one pole of a planet is seen at one instance and the observed pole may be north or south depending on the nature of inclination of the axis. If the south pole of the planet is visible when the planet is in the north celestial hemisphere then it would be erroneously characterized as north-pole according to the definition of IAU. The author modified the definition of the North Pole. According to the modified definition “the axis of a planet passing through the North Pole points towards the northern celestial hemisphere”. Following the modified definition, the south pole of a planet remains as the South Pole even when the planet is seen in the northern celestial hemisphere. When the erroneous characterization is rectified, it would be seen that no planet has retrograde rotation.
Analysis on erroneous characterisation of North Pole
It is observed that for any prograde planet, the inclination of the North Pole end of the axis of the planet with respect to the normal to equatorial plane of the sun is an acute angle (α) where the axis is close to the normal to equatorial plane. But in case of a retrograde planet, the inclination of the axis is an obtuse angle (180o- α) measured in positive direction. This aspect of inclination of the axis is remarkably distinct for prograde and retrograde planets (Table-2).
Table-2
INCLINATION IN THE RANGE OF OBTUSE ANGLE | ||
Name of planets | Inclination of the axis / Obliquity to orbit (in degrees) | Sense of rotation relative to the Sun |
Mercury | ~0.1 | Same sense |
Venus | 177.3 | Opposite sense |
Earth | 23.45 | Same sense |
Mars | 25.19 | Same sense |
Jupiter | 3.12 | Same sense |
Saturn | 29 | Same sense |
Uranus | 97.86 | Opposite sense |
Neptune | 29.56 | Same sense |
Pluto | 122.46 | Opposite sense |
Why should it be so? Conventionally the inclination of the North Pole end of the axis of the planet is considered positive in anticlockwise direction. If the North Pole end of the axis is inclined at (-α) then said inclination of the North Pole end of axis can be alternatively expressed in anticlockwise (positive) direction as (360o – α) and the south pole end of the axis would subtend an angle (180o-α) [Fig.4]. The very fact that the reported inclinations of the North Pole end of axes of retrograde planets are (180o-α) reveals that the so identified North Pole, in reality, refers only to the South Pole of the planet. An anticlockwise rotating (prograde) celestial body seen from the North Pole end would be found rotating clockwise when viewed from the South Pole end. Thus, if the south pole of an orbital body is erroneously characterized as North Pole, then the rotation of the celestial body would be erroneously characterized as having retrograde rotation. Accounting the above error in characterizing the North Pole of Venus, Uranus and Pluto it is found that these planets rotate in prograde i.e. in the same direction as the direction of rotation of the sun. The newly proposed fluid dynamics model also conforms this.
Erroneous retrograde revolution of satellites
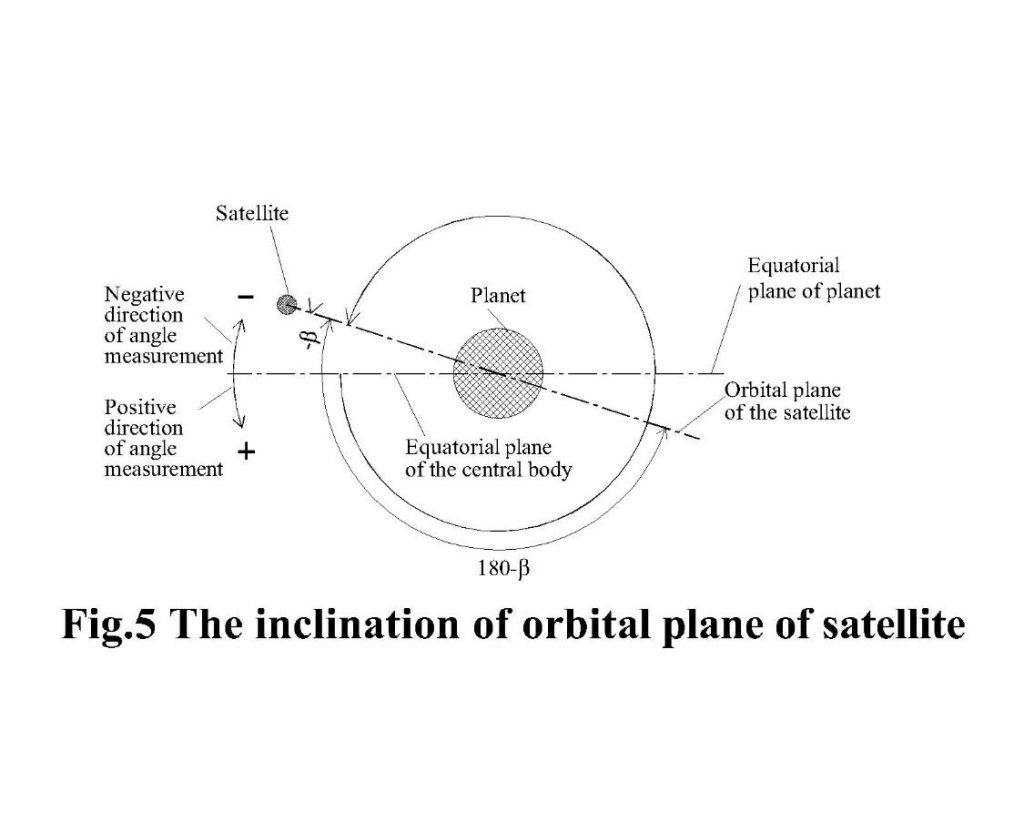
The inclinations of orbital planes of other planets are expressed with reference to the orbital plane of the earth (ecliptic) and also with reference to the equatorial plane of the sun. The interaction of the sun with planets is significant while the interaction of earth with other planets is insignificant. Thus, the inclination of orbital planes of planets relative to the equatorial plane of the sun is relevant for working out the dynamics of inclination of orbital planes. It is noticed that the orbital inclinations of most planets are acute angles where the planets are close to the equatorial plane of the sun. It is, as if, the stable orbital planes of planets lie on the equatorial plane of the sun. The orbital plane of a planet makes an inclination with the equatorial plane of the sun when the planet makes a linear oscillation perpendicular to the equatorial plane of the sun having the period of oscillation matching with the period of revolution. Hence, the inclination of orbital plane of a planet with the equatorial plane of the sun is the resultant of two component-motions, 1) orbital motion in equatorial plane of the sun and 2) linear oscillation of planet in the direction perpendicular to the equatorial plane of the sun caused by the angular oscillation of the axis of sun with respect to the axis of the nucleus of galaxy. The cause of oscillation of the axis of an orbital body is explained in a separate article of this issue by this author. The orbital planes of all satellites of a planet are also inclined to the equatorial plane of the planet; hence the inclination of orbital plane of a satellite is caused by the orbital motion of satellite and linear oscillation of satellite perpendicular to the equatorial plane of its planet. The linear oscillation of satellites is caused by the angular oscillation of the axis of the planet with respect to the axis of the sun. Here again the period of linear oscillation of the satellite perpendicular to the equatorial plane of its planet matches with the period of revolution of the satellite. The resultant orbital plane of the satellite makes an inclination with the equatorial plane of its planet.
When the axis of the earth oscillates with reference to the axis of the sun, the associated extra nuclear space structure of the earth also makes an angular oscillation which causes spatial linear-oscillation of the space fluid around the equatorial plane of the earth. The moon being located in the equatorial plane of the earth gains a drive force from the linear oscillation of the space fluid of the earth causing oscillation of the moon perpendicular to the equatorial plane of the earth (Fig.5). The resultant of orbital motion and perpendicular linear oscillation of a moon makes its orbit inclined to the equatorial plane of the earth. Like the angular oscillation of the axis of the earth, the axes of other planets oscillate with respect to the axis of the sun causing linear oscillation of their satellites perpendicular to the equatorial plane of its planet. The matching period of linear oscillation with the period of revolution causes inclination of the orbits of satellites. This makes orbital inclination of satellites with respect to the equatorial plane of their planet. Depending on the phase difference between the linear oscillations, the angle of inclination of orbital planes of satellites could be positive or negative. The anticlockwise inclination is conventionally taken as positive and that in clockwise direction is considered negative. The negative inclination –β of the orbital plane of the satellite when measured in positive direction becomes 180o- β. While satellites remain close to the equatorial plane of its planet, the inclination of the orbital plane of the satellite would be an acute angle either in positive or in negative direction. It is necessary to express the angle of inclination of all satellites of a planet from one reference end of the planet, where both positive and negative values are feasible. The reported inclination of orbital planes of satellites in retrograde revolution is given erroneously as 180o- β instead of -β.
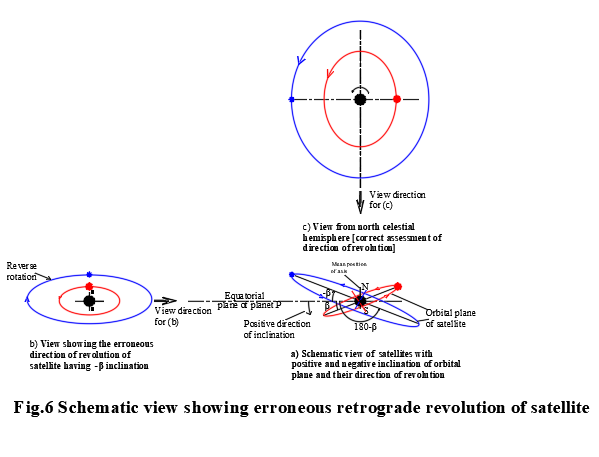
The direction of revolution of satellites is clockwise (retrograde) when the angles of inclination of the orbital plane of satellites are negative. Figure-6 shows the schematic view of two satellites having positive and negative inclination of their orbital planes. Consider two satellites rotating in anticlockwise direction (prograde) viewed from the North Pole end of the planet. But the observational conclusion changes when viewed close to the equatorial plane. The satellite having its inclination of the orbital plane in positive direction (anticlockwise) shows prograde revolution and the satellite having negative inclination (clockwise) of its orbital plane shows retrograde revolution. Thus, the observational conclusion is changed from the reality that both satellites have prograde motion. In fact no satellite revolves in retrograde when viewed on the north end side of the equatorial plane of the planet. The fact is now described in relation to Fig.6.
Most satellites revolve in prograde. However, few satellites exhibit retrograde motion tables-3 and table-4. The new fluid mechanics explaining the dynamics of different motions is dealt with in a separate article by this author in this issue. The new fluid dynamics has scope of explaining all kinds of motions of celestial bodies and leaves nothing for chance. According to the new fluid dynamics, retrograde rotation or revolution is not feasible even for a captured orbital body. On the strength of the newly proposed fluid dynamics having wider scope of explaining different motions of orbital bodies, this author anticipated some error in the characterization of retrograde revolution of satellites.
Table-3 ALL ORRBIT INCLINATIONS AT OBTUSE ANGLE HAS RETROGRADE REVOLUTION | ||||||
Name of Satellites | Orbit inclination in degrees | Direction of revolution | Name of satellites | Orbit inclination in degrees | Direction of revolution | |
Moon | 5.145 | Direct | Janus (SX) | 0.14 | Direct | |
Calypso(SXIV) | ~0 | Direct | ||||
Phobos | 1.08 | Direct | Telesto(SXII) | ~0 | Direct | |
Deimos | 1.79 | Direct | 0.2 | Direct | ||
Phoebe(SIX) | 175.3 | Retrograde | ||||
Io (JI) | 0.040 | Direct | ||||
Europa(JII) | 0.470 | Direct | Miranda(V) | 4.22 | Direct | |
Ganymede(JIII) | 0.195 | Direct | Ariel(I) | 0.31 | Direct | |
Callisto(JIV) | 0.281 | Direct | Umbriel (II) | 0.36 | Direct | |
Metis(JXVI) | 0.0 | Direct | Titania (III) | 0.10 | Direct | |
Adrastea(JXV) | 0.0 | Direct | Oberon (IV) | 0.01 | Direct | |
Amalthea(JV) | 0.40 | Direct | Cordelia(VI) | 0.1 | Direct | |
Thebe(JXIV) | 0.8 | Direct | Ophelia(VII) | 0.1 | Direct | |
Leda(JXIII) | 27 | Direct | Binca(VIII) | 0.2 | Direct | |
Himalia(JVI) | 28 | Direct | Cressida(IX) | 0.0 | Direct | |
Lysithea(JX) | 29 | Direct | Desdemona(X) | 0.2 | Direct | |
Elara (JVII) | 28 | Direct | Juliet(XI) | 0.1 | Direct | |
Ananke(JXII) | 147 | Retrograde | Portia(XII) | 0.1 | Direct | |
Carme (JXI) | 163 | Retrograde | Rosalind(XIII) | 0.3 | Direct | |
Pasiphae(JVIII) | !48 | Retrograde | Belinda(XIV) | 0.0 | Direct | |
Sinope(JIX) | 153 | Retrograde | Puck(XV) | 0.3 | Direct | |
S/1997 U1 | highly inclined | Retrograde? | ||||
Mimas(SI) | 1.53 | Direct | ||||
Enceladus(SII) | 0.02 | Direct | S/ 1997 U2 | highly inclined | Retrograde? | |
Tethys(SIII) | 1.09 | Direct | ||||
Dione (SIV) | 0.02 | Direct | Naiad (NIII) | 4.74 | Direct | |
Rhea (SV) | 0.35 | Direct | Thalassa (NIV) | 0.21 | Direct | |
Titan (SVI) | 0.33 | Direct | Despina (NV) | 0.07 | Direct | |
Hyperion(SVII) | 0.43 | Direct | Galatea (NVI) | 0.05 | Direct | |
Iapetus(SVIII) | 7.52 | Direct | Larissa (NVII) | 0.20 | Direct | |
Pan (SXVIII) | …… | Direct | Proteus (NVIII) | 0.55 | Direct | |
Atlas (SXV) | ~ 0 | Direct | Triton (NI) | 156.834 | Retrograde | |
Prometheus(SXVI) | 0.0 | Direct | Nereid (NII) | 7.23 | Direct | |
Pandora(SXVII) | 0.0 | Direct | ||||
Epimetheus(SXI) | 0.34 | Direct | Charon | 96.56 | Retrograde? | |
Table-4 ACTUAL ORBITAL INCLINATIONS OF RETROGRADE SATELLITES EVALUATED FROM PRESENTLY USED VALUES | ||
Retrograde satellites | Presently known values in degrees4 | Corrected values from proper reference in deg. |
of Jupiter Ananke (JXII) Carme (JXI) Pasiphae (JVIII) Ssinope (JIX) | 147 163 148 153 | – 33 or + 327 – 17 or + 343 – 32 or + 328 – 27 or + 333 |
of Saturn Phoebe (SIX) | 175.3 | – 4.7 or + 355.3 |
of Uranus S/1997 U1* S/1997 U2* | highly inclined – (small acute angle) (value not known) | |
of Neptune Triton (N1) | 156.834 | – 23.166 or + 336.834 |
It is interesting to find that the four outermost moons of Jupiter (Ananke, Carme, Pasiphae and Sinope) and Phoebe, the outermost moon of Saturn have retrograde revolution [4]. No plausible explanation is available for such a distinct phenomenon. The author has explained the cause of negative inclination of outer satellites in a separate article in this issue.
Conclusion
The new finding on discrete nature of orbits in the solar system opens up new scope of finding similarity between solar system and atomic system. The nature of anticipated discrete orbit of electrons in atomic structure could be improved in the light of the nature of discrete orbit of planets and satellites thereby the new atomic model can come closer to reality and can be made conceptually sound in justifying atomic phenomena.
We observe different motions of celestial bodies. The motions of orbital bodies seen from earth are only relative motions relative to the earth. The earth is not an influencing celestial body inducing motions of all planets and satellites. The earth has only the force inducing interaction with the moon of the earth hence it is possible to develop the dynamics of the Earth-Moon system by the motions of the moon relative to the earth. For the dynamics of the solar system, all kinds of motion of planets are required to be characterized with reference to the sun and all kinds of motion of satellites are required to be characterized with reference to their planet for working out the dynamics of orbital bodies. The new light of thought given in this paper has scope of discovering new force interactions to justify the motions of celestial bodies.
Reference
- https://philosophyofnature.org.in/extrapolation-of-bodes-lawtowards-unravelling-the-mysteries-of-the-solar-system.
- https://philosophyofnature.org.in/new-interactions-of-mass-and-space-is-the-cause-of-gravity.
- https://philosophyofnature.org.in/electric-and-non-electric-charges-and-their-inter-conversion.
- https://www.britannica.com/science/retrograde-motion.
