INSTITUTE OF PHILOSOPHY OF NATURE
Abstract
Bode’s Law describes the correlation of the distances of planets from the sun which is unique of its kind. Though Bode’s Law was verified for the Uranus (which was discovered subsequently) and further became applicable in finding the asteroid belt, many astronomers dismiss Bode’s Law as a mere coincidence. Today it has no connection with modern astronomy. In this paper a new model in the light of Bode’s Law is proposed which works well uniformly for the planets of the sun and the satellites of respective planets. The author postulates an undulated gravity field with humps providing energy wells for the stable locations of the orbital bodies. Thus, a kind of discrete orbit system appears valid for the solar system like the atomic system. Key words: Bode’s law, solar system, planets, satellitesIntroduction
In 1770 Titius developed an interesting mathematical correlation among the distances of the planets from the sun. This finding was first published and made famous by J.E. Bode, the then Director of Berlin observatory and was subsequently known as Bode’s Law [1]. The law states: Take numbers 0, 3, 6, 12, 24, 48, 96 and 192 each of which apart from the first is double its predecessor. Now add 4 to each giving 4, 7, 10, 16, 28, 52, 100 and 196. Taking the earth’s distance from the sun as 10, these figures give the distances of the remaining planets with remarkable accuracy as shown in Table -1. When Bode proposed this correlation, the Uranus had not been discovered, but later in 1781 when the Uranus was discovered by Sir William Herschel, it exactly fitted into the scheme. This gave impetus to Bode’s Law and a serious search was initiated for the missing planet in the gap between the mars and the Jupiter. In 1800 AD six astronomers met in Germany to organise a systematic hunt for the missing planet. The association thus formed was unofficially popular under the name ‘Celestial Police’. However, the first asteroid was discovered in January 1, 1801 by an Italian astronomer, Giuseppe Piazzi in the island of Sicily. This was first considered to be a tailless comet. Subsequently Karl Friedrich Gauss, a German mathematician made use of the large number of observations of Piazzi and established that the new little planet fitted well into the scheme of Bode’s Law. Here, one may notice that, Bode’s Law not only was a mathematical correlation of the planets known then but has been verified for the location of the Uranus and further proved useful in discovering the asteroids. But when the Neptune was discovered in 1846 and the Pluto in 1930 they were found to deviate from Bode’s correlation. Moreover, it is not applicable to the satellite systems of the planets. This made many astronomers dismiss Bode’s Law as mere coincidence. Until today Bode’s Law has no connection with the modern, totally unofficial “Spode’s Law” which states broadly that if things can go wrong they do [2]. No doubt, Bode’s mathematical correlation faced limitations for the complete observation of orbital bodies in solar system but these limitations may not be enough to discard the law totally because most of the manmade laws of nature have limitations while working in a limited frame of reference. The author’s feeling here is that Bode’s Law cannot totally be meaningless. He believes that, Bode’s Law as stated by Titius and Bode is perhaps an incomplete description of the correlation for the entire solar system towards the placement of orbital celestial bodies and possibly the law can be modified to overcome its limitations. For example, the placement of electrons in the atomic structure is complete by consideration of both shells and sub-shells. Thus, any proposal for a quantum theory dealing with the shells alone could have been discarded at the equal footing of Bodes’s Law due to incomplete answer for the observed energy level events. In view of this, the author has made a humble approach to supplement Bode’s Law towards a complete satisfactory correlation of the orbital bodies in the solar system.Observation of quantum correlation for planetary discrete orbits – a new finding:
A glance at the distances of the planets from the sun (Table-1) and the orbital distances of the satellites of the Jupiter (Table-2) gives an impression as if the orbital bodies have an inherent tendency to maintain an outwardly expanding order of spacing. The phenomenon approximates the placement of orbital bodies in some geometrical progression (GP) series. Bode’s Law which correlates the distances of planets from the sun also speaks of this fact. Bode’s Law can be written in the following mathematical form. Dn = (4+3 x 2n)/10 (1.1) Where, Dn is the distance of the nth orbit from the sun (except for the mercury) in astronomical units (AU) n is an integer and can have values 0,1,2,3 ………. We may generalise the expression by writing Dn = (a + b cn)k Where, a,b,c are constants of the central gravitating body k is the scale constant ak is the distance of the mercury from the sun The satellites of the Jupiter also having the outwardly expanding order of placement is quite tempting for finding out a GP series correlating the placement of satellites. Here, it is seen that, a considerable number of satellites do respond well for their placement correlating through a GP series while the others deviate considerably. One might ask a serious question – why after all a group of planets and satellites respond to GP series for their placement? The response is so striking that it just cannot be ignored for being a coincidence. At this juncture, the locations of the satellites of the Jupiter and the Uranus, those exhibiting different norms (those having a misfit in the GP series) may be examined in detail for finding some clue. It is noticed that some of the above satellites exhibit a tendency of forming closer groups around certain orbits. Referring to Fig.1, it may be seen that, around a distance of 1.18 x 107 km from the Jupiter, the satellites form a grouping with closer intervals. In the similar manner around a distance of 0.646 x 105 km from the Uranus, the satellites of the Uranus also form similar grouping.
TABLE-1 |
||
BODE’S LAW |
||
PLANET DISTANCES OF PLANETS FROM SUN(SCALE 10 UNITS = 1 au = 1.494 x 108 kms) |
||
| Planets | According to Bode’s law | Actual |
| MERCURY | 4 | 3.9 |
| VENUS | 7 | 7.2 |
| EARTH | 10 | 10 |
| MARS | 16# | 15.2 |
| JUPITER | 52 | 52 |
| SATURN | 100 | 95.4 |
| URANUS | 196 | (191.8) * |
TABLE-2 |
|||
ORBITAL DISTANCES OF SATELLITES OF JUPITER |
|||
| Sl. No | Satellite(name) | Revolution period (in sideral days) | Semi major axis in kms |
| 1 | Thebe | 0.675 | 2.22 x 105 |
| 2 | Io | 1.769 | 4.25 x 105 |
| 3 | Europa | 3.551 | 6.76 x 105 |
| 4 | Ganymede | 7.155 | 1.08 x 106 |
| 5 | Callisto | 16.689 | ** 1.90 x 106 |
| 6 | Leda | 240 | ** 1.11 x 107 |
| 7 | Himalia | 251 | ** 1.15 x 107 |
| 8 | Lysithia | 260 | ** 1.17 x 107 |
| 9 | Elara | 260 | ** 1.18 x 107 |
| 10 | Ananke | 617 | ## 2.08 x 107 |
| 11 | Carme | 692 | ## 2.24 x 107 |
| 12 | Pasiphae | 735 | ## 2.33 x 107 |
| 13 | Sinope | 758 | ## 2.38 x 107 |
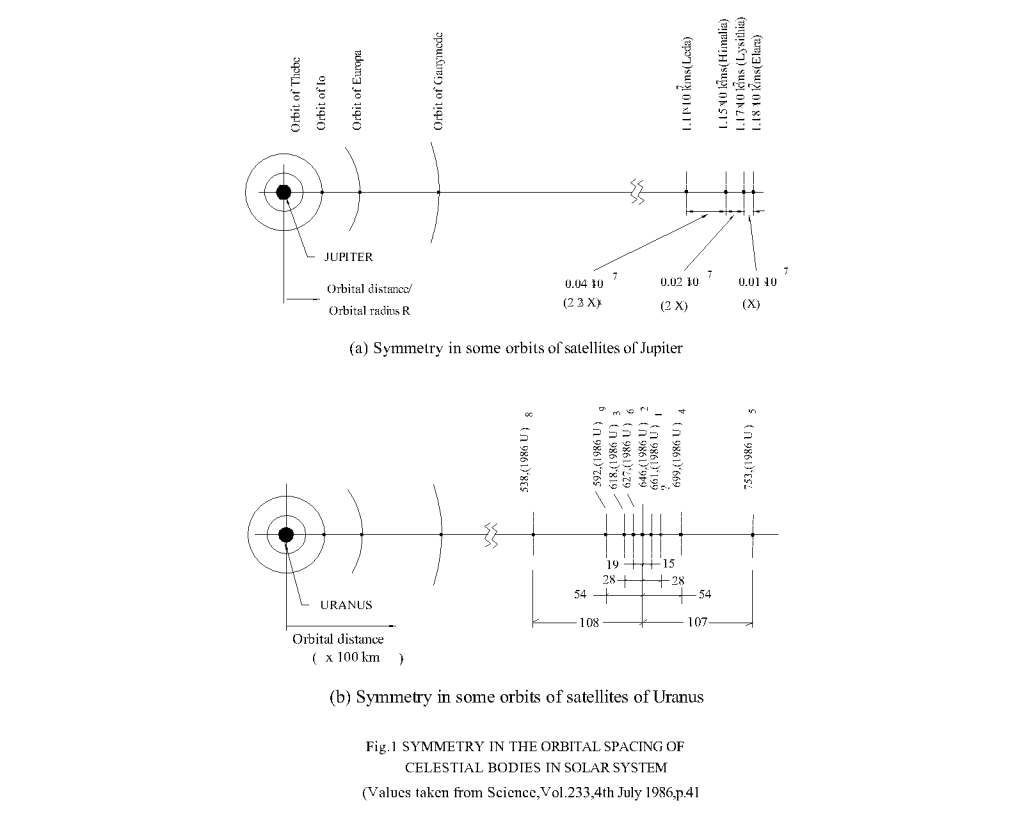
The orderly spacing of the satellites those don’t respond to the locations conforming to the GP series originating from the planet are as if they were placed in another GP series originating from a principal orbit. These placement sites may be called as sub-orbits of the principal orbit.
In the light of the new concept of sub-orbits of a principal orbit, a new model for correlating the distances of orbital bodies is proposed by the author in Fig.2. This new thinking goes in coherence with the existence of many orbitals associating an orbit in the atomic system. However, it may be controversial to think that the sub-orbits/sub-shells of an orbit to have different mean radial distances in contrast to the established fact in atomic system, where the orbitals/sub-shells of an orbit/shell have essentially the same mean radius but with different geometry of the orbit. At this stage without looking for a unification of the atomic and the solar system, let us only borrow the orbital/sub-shell concept from the atomic system to the planetary system just like the borrowed orbital electron concept taken from the planetary system and deal the two systems separately according to their realities.
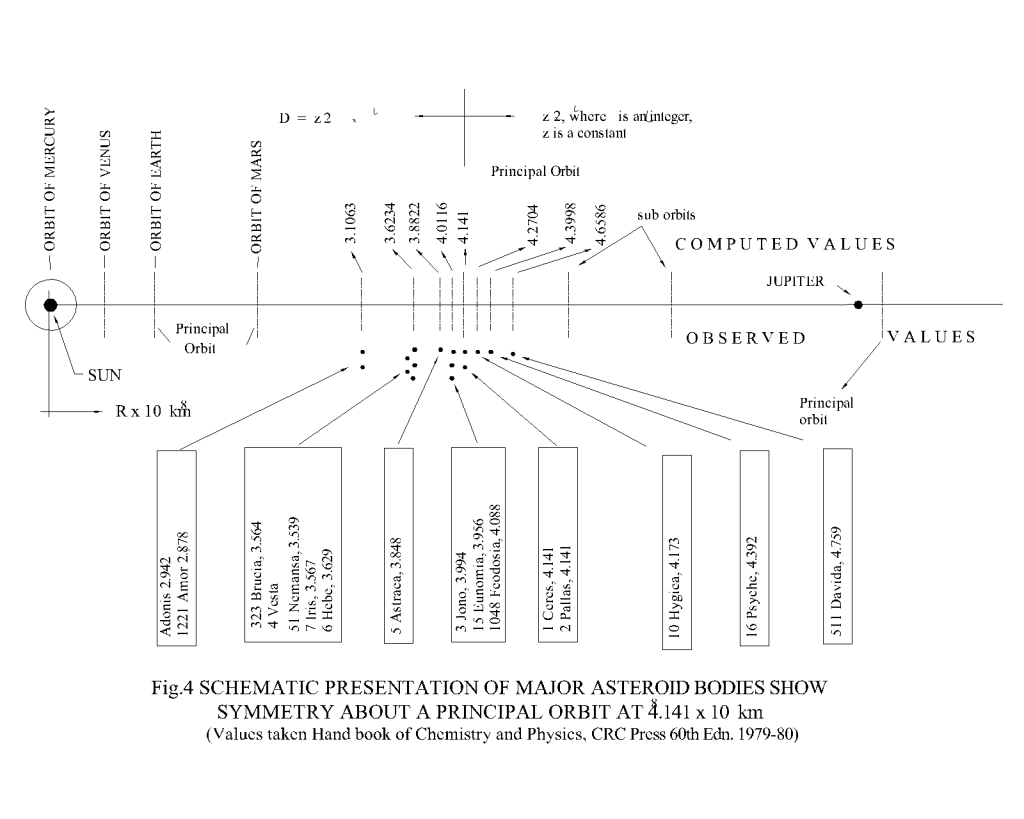
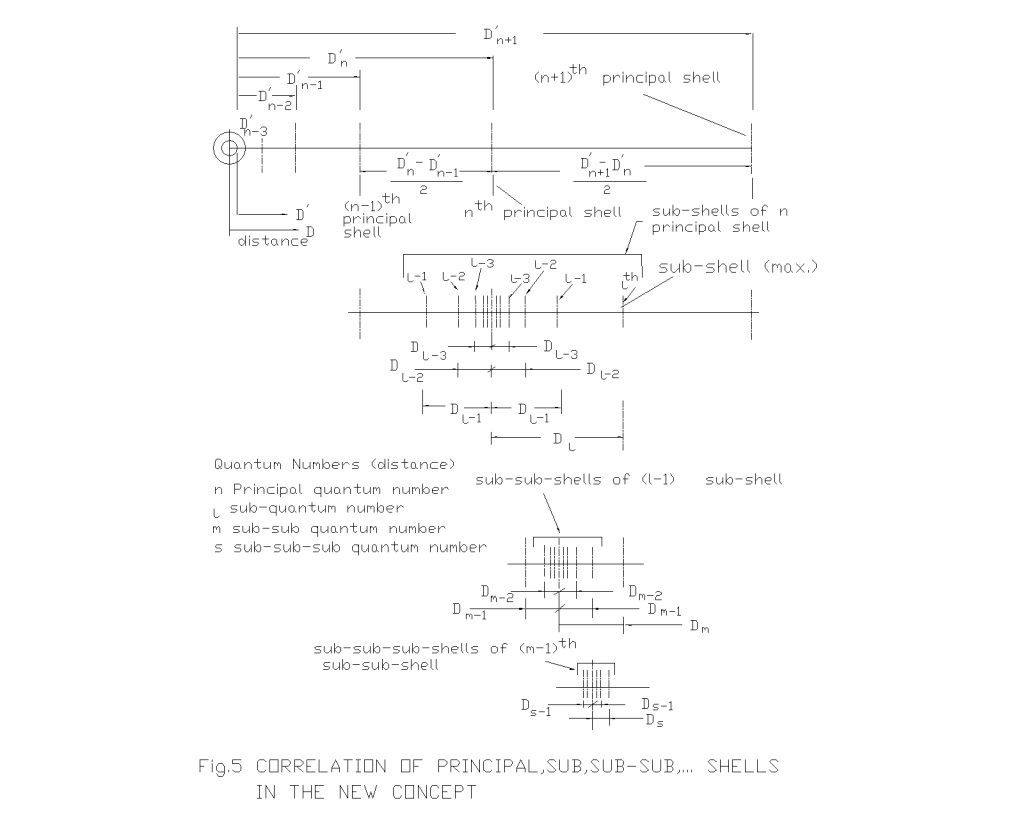
The shell, sub-shells/sub-orbits of planetary (newly identified) and atomic (existing) systems are shown in Fig.3. The existence of sub-orbits can be better examined from the analysis of the placement of asteroids between the mars and the Jupiter. Surprisingly enough, the asteroids too reveal this fact remarkably well. A schematic presentation of the locations of the major asteroids of the solar system is shown in Fig.4. It may be seen clearly from the distances of the asteroids3 that the spacing of sub-orbits/sub-shells of a principal orbit/shell also goes on expanding outwardly in either direction similar to the outward expansion of the spacing of the principal orbits. Now, with this new concept of orbits and sub-orbits, it becomes easier to develop a mathematical formulation of the GP-series to establish the hidden relationship of the orbits/shells and the sub-orbits/sub-shells.
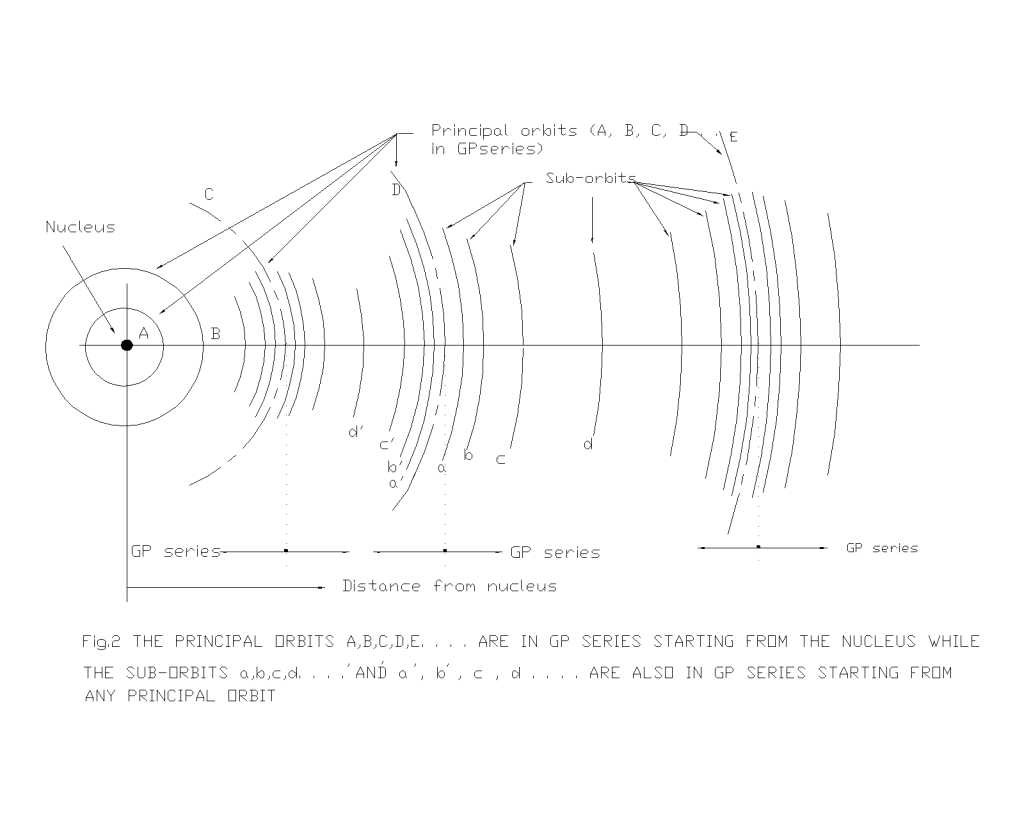
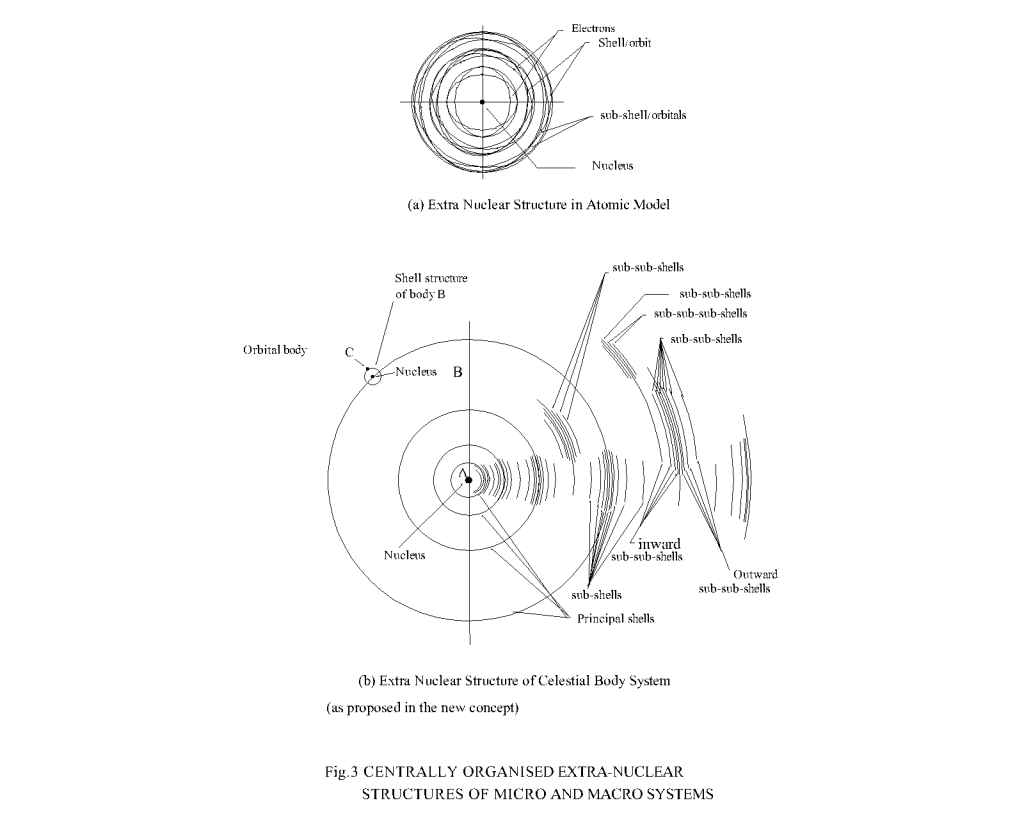
New mathematical correlation of orbits and sub-orbits.
The GP series given in eqn. (1.2) ascertain the positions of all principal orbits with reference to any one of the principal orbits.
D’n = z x 2n (1.2)
Where,
D’n is the distance of nth principal orbit of the central gravitating body measured from any (conventionally innermost) principal orbit/shell as the reference..
z is the nucleus constant of the central gravitating body.
n is an integer, conventionally can have values 0, 1, 2, 3 ….
Again the distances of sub-orbits/sub-shells (Dl) measured from the concerned principal orbit/shell can be expressed as:
Dl = z1cl1 (1.3)
Where, Dl = the distance of the lth sub-orbit/sub-shell measured radially from the concerned
principal orbit/shell.
z1 is a function of the nucleus constant of the central gravitating body.
c1 is the constant of the principal orbit / shell
l is an integer which can have values … -3, -2, -1, 0, 1, 2, 3 …
By computation and analysis of the actual distances of orbital bodies in the solar system it is found that,
z1 = z and c1 = 2
Hence, Dl = z.2l (1.4)
From eqn. (1.3) and eqn. (1.4) it is seen that the principal orbit/shell and the sub-orbit /sub-shell are decided from the nucleus constant only. Here, one might like to draw a simile with the nucleus constant of the atomic system.
Limiting values of the integers n and l
The integers n and l used for determination of the principal orbits/shells and sub-orbits/sub-shells respectively need to be understood for their limiting values and their inter relation. Consider any nth principal orbit/shell in Fig.5.
For nth shell, D’n = z. 2n
For (n-1)th shell, D’n-1 = z. 2n-1
For (n+1)th shell, D’n+1 = z. 2n+1
Thus the spacing between (n-1)th principal orbit/shell and the nth principal orbit/shell is given by:
D’n – D’n-1 = z. 2n – z .2n-1 = z. 2n-1
And the spacing between the nth principal orbit and the (n+1)th principal orbit is given by:
D’n+1 – D’n = z. 2n+1 – z. 2n = z. 2n
Hence, D’n – D’n-1 = (1/2) (D’n+1 – D’n)
Theoretically the series z 2n and z 2l can reach infinity. But this does not happen in reality as there are other celestial bodies in the proximity. When the principal orbits/shells of one celestial body go on extending outwardly, they meet the principal orbits /shells of other celestial bodies in the proximity and this limits the formation of further principal orbits/shells. Thus, the extent, to which a celestial body organises its principal orbits/shells, depends on the strength of the organising forces as well as the background conditions. Likewise the sub-orbits/sub-shells of a principal orbit/shell while having their outwardly expanding placement, find terminal limitations from either sides by the sub-orbits / sub-shells of the neighbouring orbits/shells. Now, limiting the maximum distance of sub-shells to the mid-points of the spacings of the corresponding principal shells, the maximum distance of inward (towards the central gravitating body) and outward (away of the central gravitating body) sub-orbits of a principal orbit may be written as :
(Dli Max) = (1/2) (z. 2n – z. 2n-1 ) = z. 2n-2 (1.5)
and ( Dlo Max) = (1/2) (z. 2n+1 – z. 2n) = z. 2n-1 (1.6)
Where
(DMax = the maximum distance of inward sub-orbit/sub-shell of nth principal orbit/ shell measured from the principal orbit / shell.
(Dlo Max) = the maximum distance of outward sub-orbit/sub-shell of nth principal orbit/shell measured from the principal orbit/shell.
Now from eqn. (1.4) and eqn. (1.6)
(Dli Max) = z.2(li)Max = z.2n-2
hence (li)Max= n-2
Similarly , (lo)Max= n-1
Thus, the maximum value of l = (lo)Max = n-1
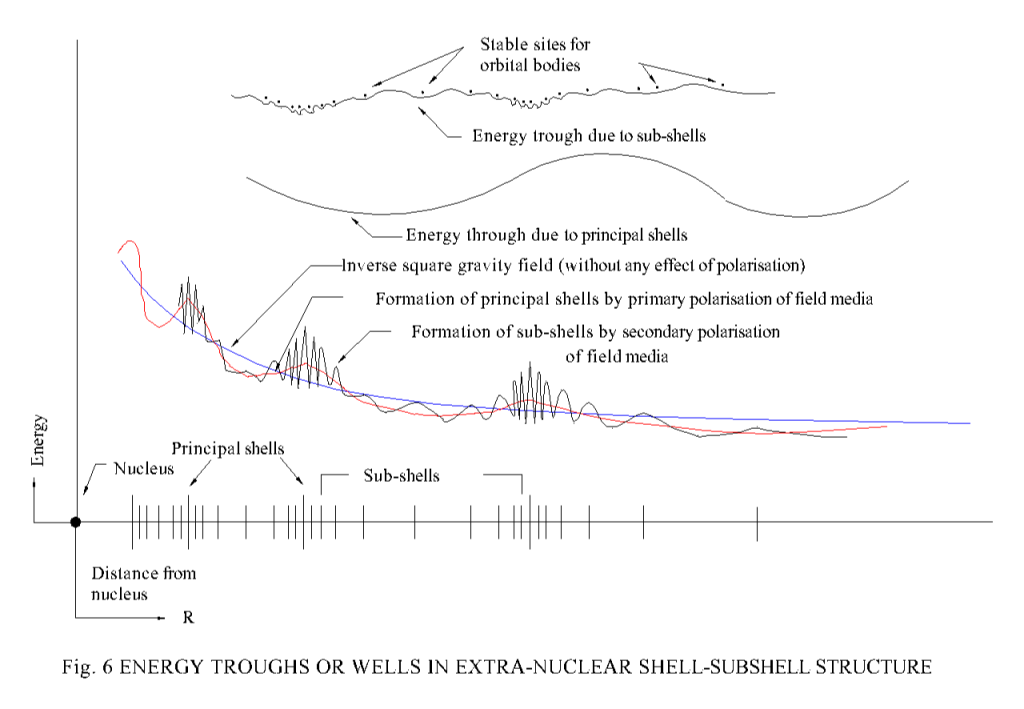
Like the formation of sub-orbits/sub-shells around an orbit/shell, the formation of sub-sub-orbits/sub-sub-shells around a sub orbit/sub-shell and so on cannot be ruled out. Perhaps these shell, sub-shell, sub-sub-shell,… features of a celestial body give rise to the formation of gravitational field humps (generating energy wells) in the extra nuclear space of a celestial body where the larger orbital bodies are trapped in the shells and sub-shells leaving the sub-sub-shells, sub-sub-sub-shells,…. for smaller bodies, like dust particles, aerosols etc., those form the rings, layer structures in upper and lower atmosphere.
The anticipated picture of the gravity field with trapping energy wells those resulting discrete placement of orbital celestial bodies surrounding a nucleus body is shown in Fig.6. Scientists working in space laboratories have greater scope of examining the nature of gravitational wells to establish this new concept.
Now, similar to the analysis of sub-shells, one may analyse the limiting conditions of sub-sub-shells, sub-sub-sub-shells… as presented in Fig.5. In the light of earlier calculations it can be shown that,
(Dl)Max = z.2n-1 =(1/2) z.2n (1.7)
(Dm)Max = z.2l-1 = (1/4) z.2n (1.8)
(Ds) Max = z.2m-1 = (1/8) z.2n (1.9)
and lMax = n-1
mMax = l-1
sMax = m-1
Where
l, m and s are the integers corresponding to sub-shells, sub-sub-shells and sub-sub-sub-shell respectively.
Let us now find the lower limit of the integer n. Theoretically the innermost shell corresponding to n= -ꭃ falls at the centre of the central celestial body. Obviously, this is beyond the continuity of extra nuclear space and thus the correlation does not hold good. The lowest limit of the shell (innermost shell) is decided by the parameters of the central gravitating body. In general, the value of (D’n)Min corresponding to nMin is very small as compared to the distances of the shells housing the orbital celestial bodies. Hence, for simplicity the distance D’n of the principal shell measured from the innermost shell can be approximated to shell radius Dn shown in Fig.7. The average value of shell radius can further be approximated to the semi-major axis of an orbital body; hence, D’n~Dn
Where
D’n = the distance of nth principal orbit/shell measured from the innermost shell.
Dn = the distance of nth principal orbit/shell measured
From the centre of the central gravitating body
i.e. the semi-major axis of the orbital body.
We may now write the general expression for the distances of the shells, sub-shells, sub-sub-shells … which corresponds to the distances of orbital bodies from the central body.
D = z.2n ±z.2l ± z.2m ±z.2s ±……….
or
D = z(2n ±2l ±2m + 2s ±…….) (1.10)
Where
D is the distance of the orbital body from the centre of the central gravitating body (i.e. the semi-major axis of the orbital body by approximation)
z is nucleus constant
n, l, m and s are integers / quantum numbers of shells, sub-shells, sub-sub-shells and sub-sub-sub-shells respectively
which can have values … -5, -4, -3, -2, -1, 0, 1, 2, 3 …
with a condition:
lmax = n-1, mmax= l-1, Smax = m-1 …..

The values of constant z for the sun and different planets in the solar system have been evaluated while trying to fit the model with the available data. The value of z for the sun has been easily obtained from the detailed study of symmetry of orbits of asteroids. From this symmetry the location of one of the principal shells can be speculated to be around 4.141 x 108 km from the sun.
Thus,
Dn = 4.141 x 108 km for n = 3
(By fixing n = 0 for the mercury)
Hence, z = Dn/2n = 0.5176 x 108 km
For evaluation of orbital distances of celestial bodies, it may be enough to work-out up to sub-shells only. Thus, eqn. (1.10) may be reduced to
D = z.2n ±z.2l = z (2n ± 2l) (1.10a)
The complete shell, sub-shell locations of orbital bodies in solar system have been calculated using eqn. (1.10a) and presented graphically in Fig.8, Fig.9, Fig.10, Fig.11 and Fig.12 for different systems. It may be seen from all these figures that the placement of celestial bodies agrees well to the general model as proposed here. The deviations of the computed results from the actual ones (table-3, table-4, table-5, table-6 and table-7) are well within the limits of approximations made in the computation as well as in the uncertainty in measurements. And further the celestial bodies in the orbits
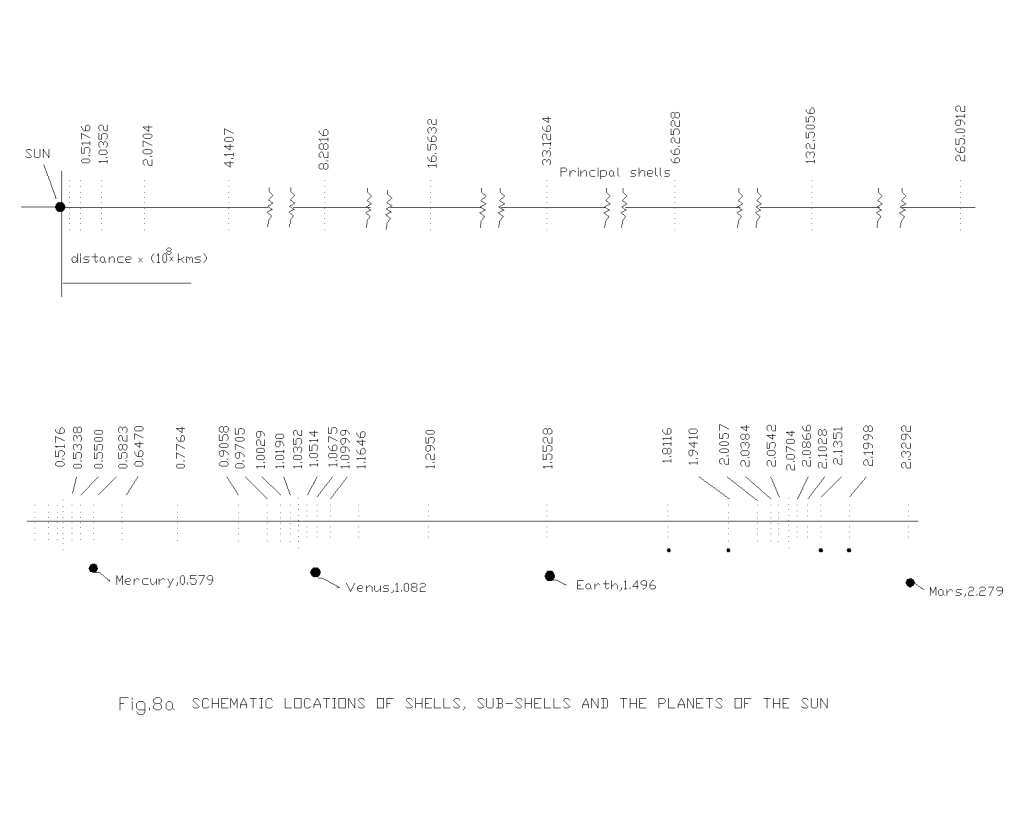
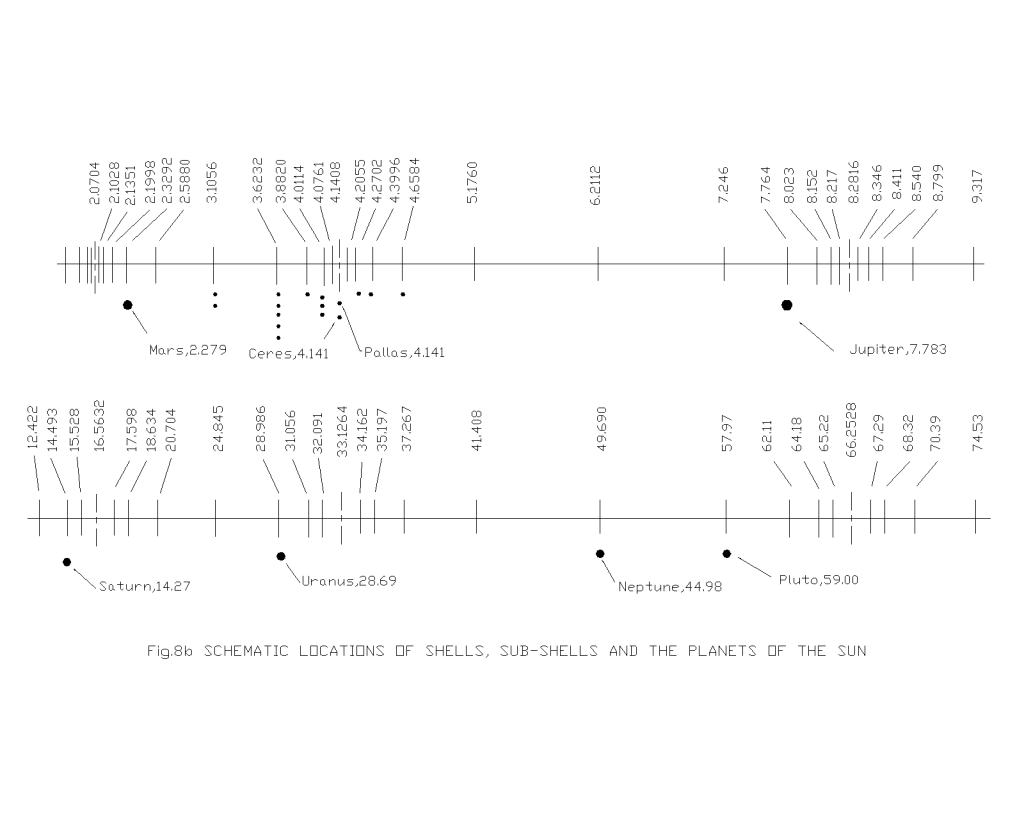
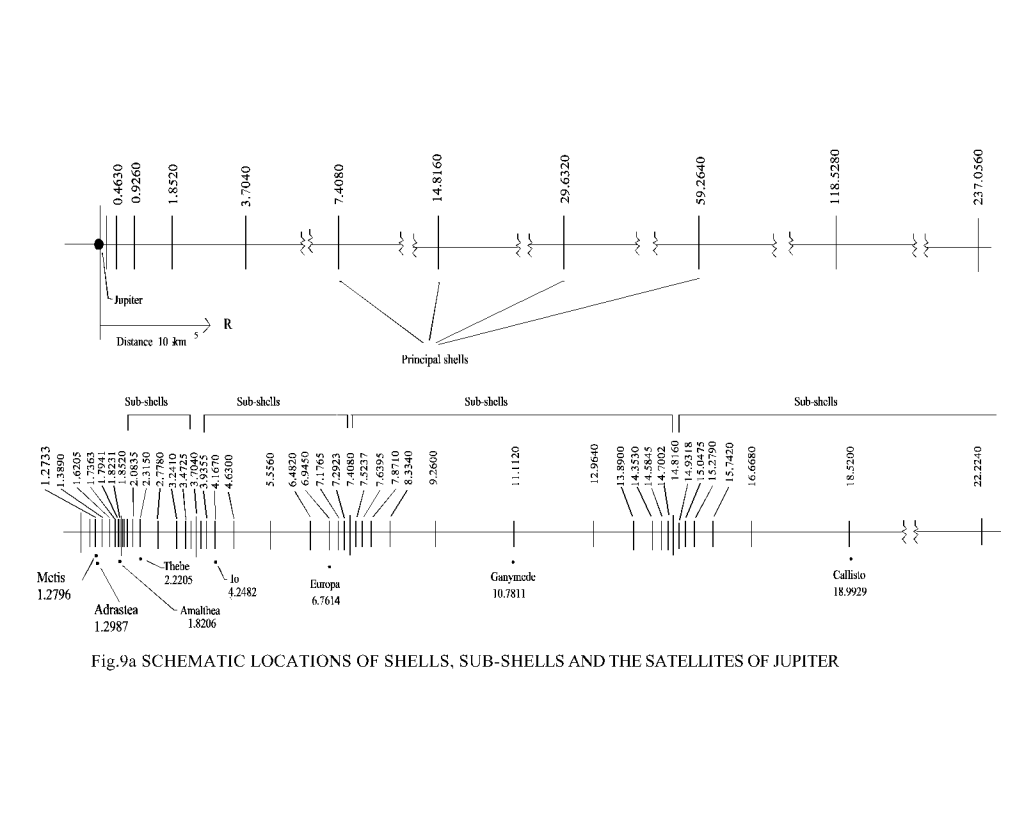
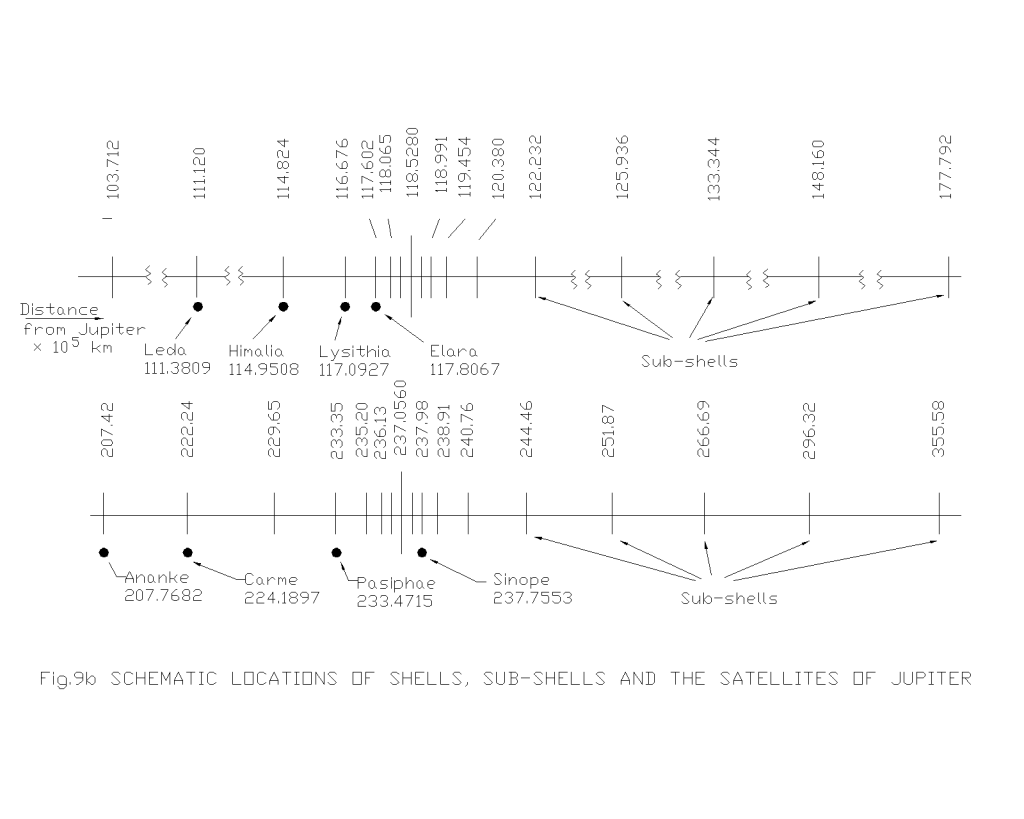
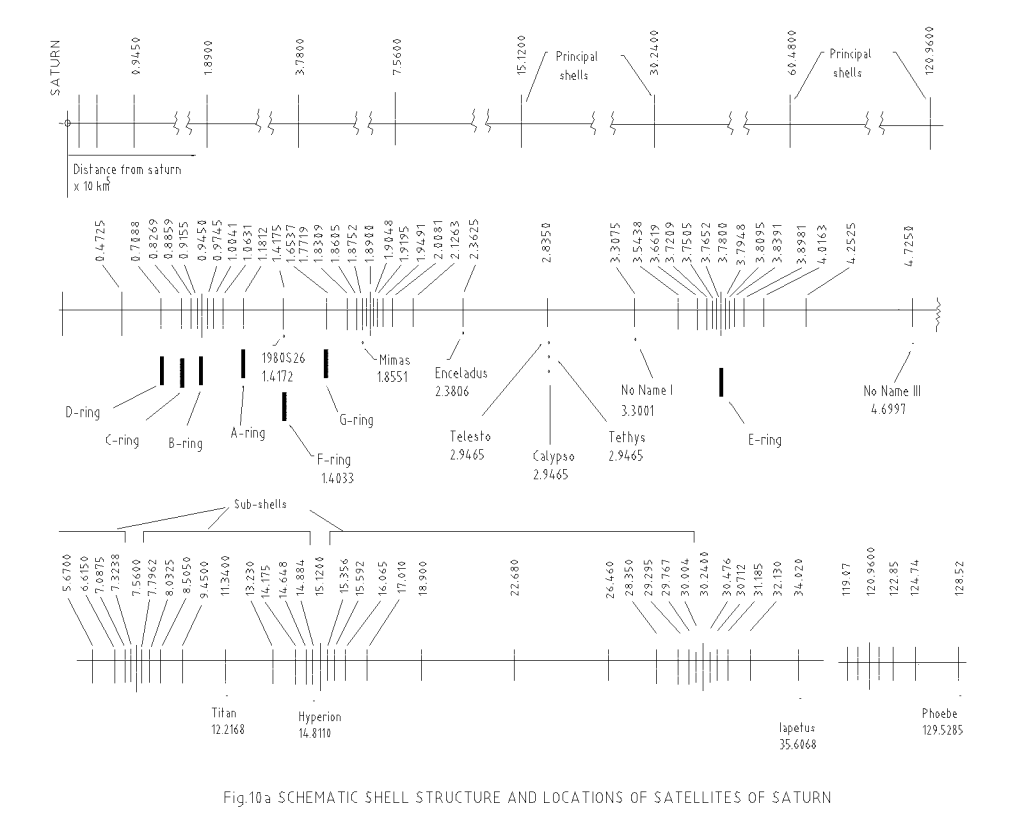
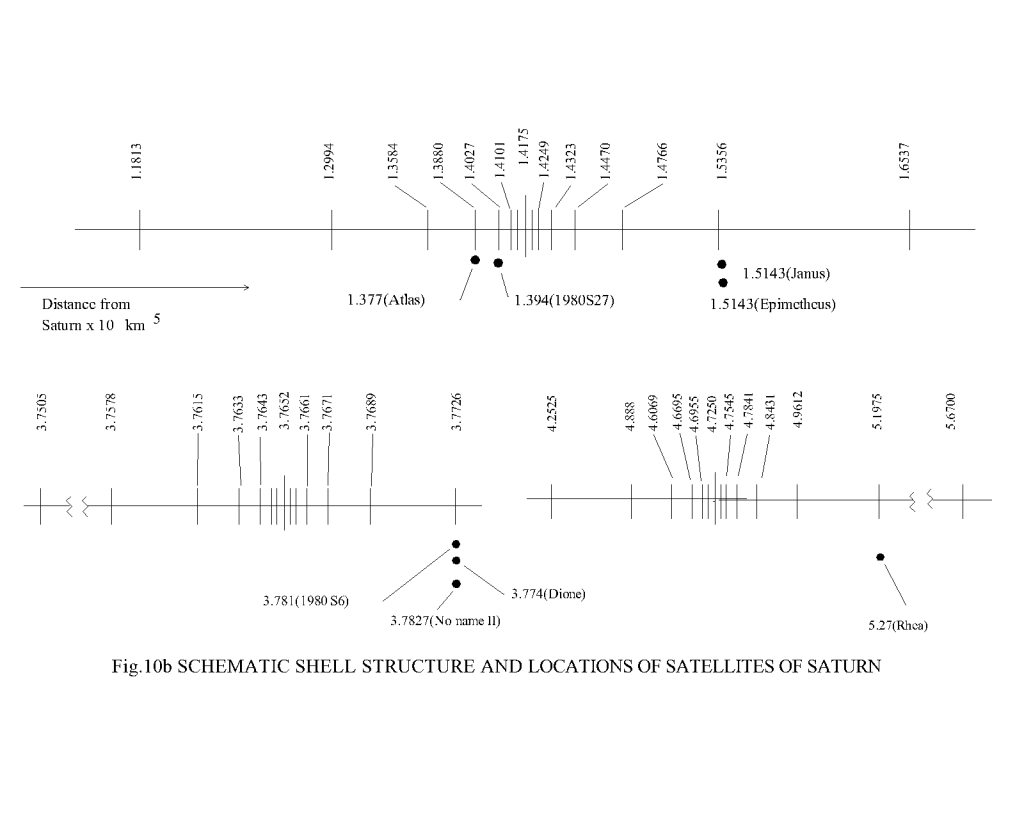
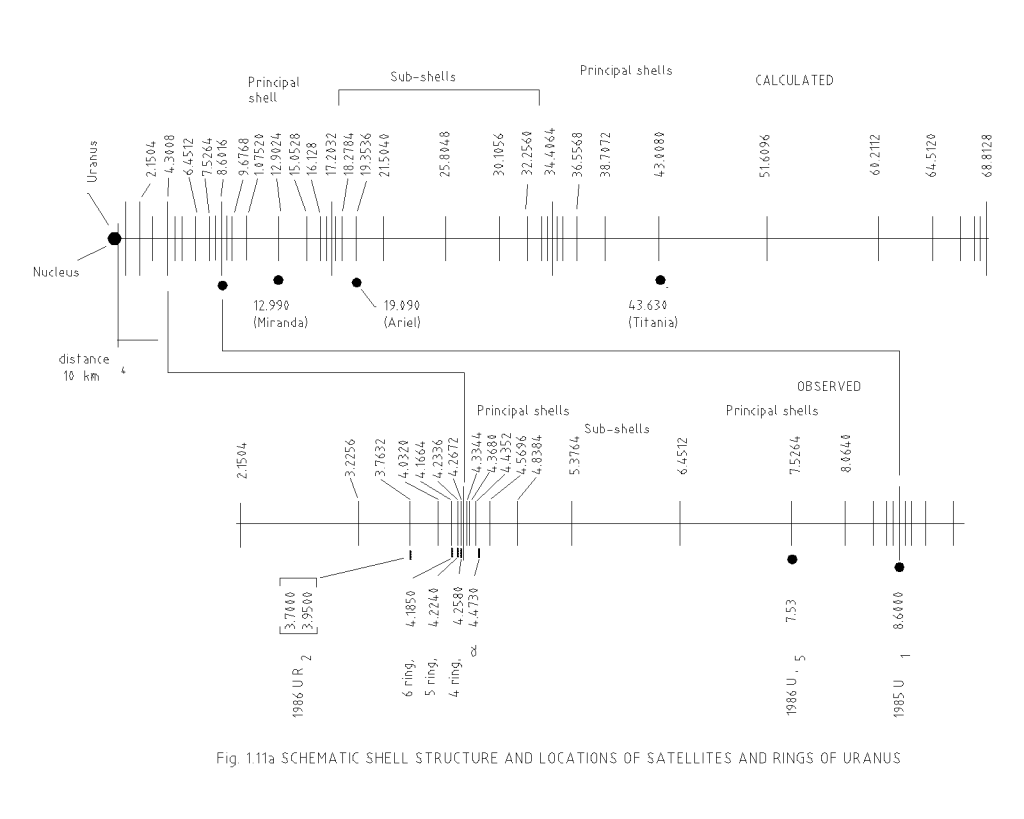
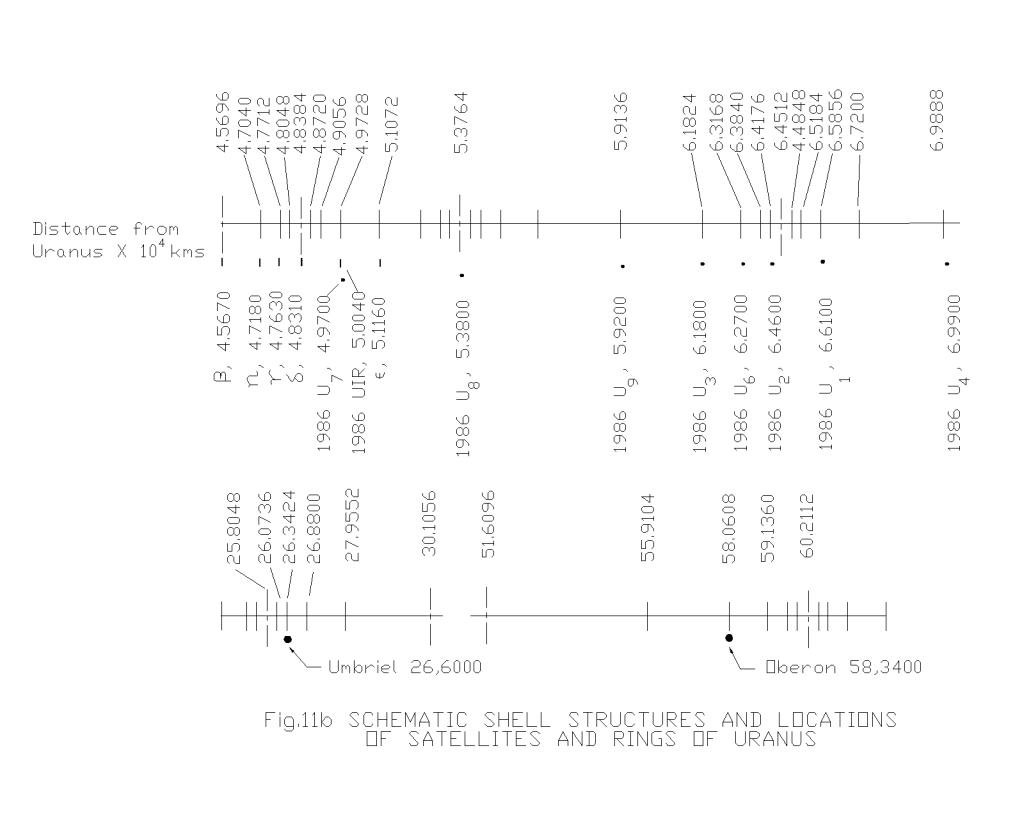
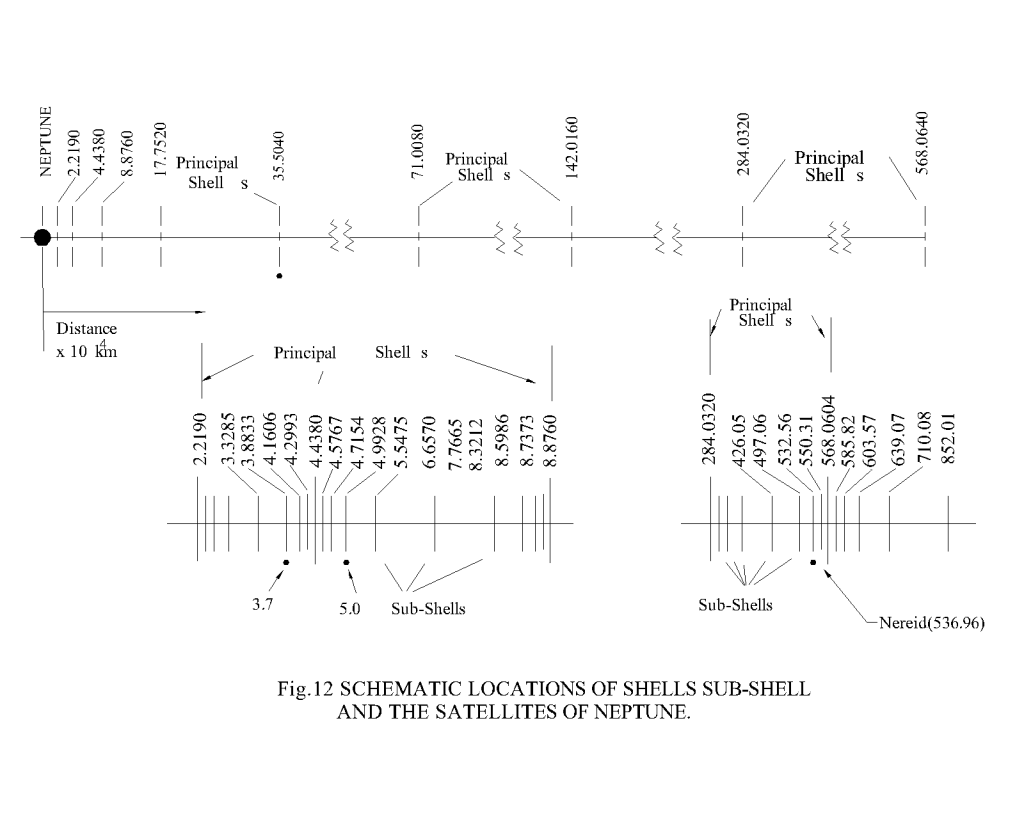
TABLE-3 [3] |
||||
PERCENTAGE DEVIATION IN THE PREDICTED DISTANCES OF THE PLANETS AND MAJOR ASTEROIDS FROM THE SUN |
||||
| Name of Plants & Asteroids | Observed distance x 108 km | computed distance x 108 km | Difference x 108 km | Percentage deviation |
| Mercury | 0.579 | 0.5823 | +0.0033 | +0.57 |
| Venus | 1.082 | 1.0675 | – 0.0145 | -1.34 |
| Earth | 1.496 | 1.5528 | +0.0568 | +3.79 |
| Mars | 2.279 | 2.3292 | +0.0502 | +2.20 |
| Adonis | 2.942 | 3.1056 | ……… | …….. |
| Amor | 2.878 | ……. | ……… | …….. |
| Brucia | 3.564 | 3.624 | ……… | …….. |
| Vesta | 3.531 | …….. | ……… | …….. |
| Nemansa | 3.539 | …….. | …….. | …….. |
| Iris | 3.567 | …….. | …….. | …….. |
| Hebe | 3.629 | …….. | …….. | …….. |
| Asbraca | 3.848 | 3.8820 | 0.0342 | +0.89 |
| Juno | 3.994 | …….. | …….. | …….. |
| Eunomia | 3.956 | 4.0114 | …….. | …….. |
| Feodosia | 4.008 | …….. | …….. | …….. |
| Ceres | 4.141 | 4.1408 | …….. | …….. |
| Pallas | 4.141 | …….. | …….. | …….. |
| Hyglea | 4.173 | 4.2704 | +0.0974 | +2.33 |
| Psyche | 4.392 | 4.3998 | +0.0078 | +0.17 |
| Dayida | 4.759 | 4.6586 | -0.1004 | -2.11 |
| Jupiter | 7.783 | 7.764 | -0.0190 | -0.24 |
| Saturn | 14.27 | 14.493 | +0.2230 | +1.56 |
| Uranus | 28.69 | 28.986 | +0.2960 | +1.03 |
| Neptune | 44.98 | 49.69 | +4.710 | +10.47 |
| Pluto | 59 | 57.97 | -1.0300 | -1.74 |
TABLE-4 |
|||||
PERCENTAGE DEVIATION IN THE PREDICTED DITANCES OF THE SATELLITES of JUPITER |
|||||
| No | Name | Observed distance * x 105 km | Computed distancex 105 km | Difference x 105 km | Percentage deviation |
| 16 | Metis | 1.2796 | 1.2733 | -0.0063 | -0.806 |
| 14 | Adrastea | 1.2987 | 1.2733 | -0.0254 | -1.956 |
| 5 | Amalthea | 1.8206 | 1.8231 | +0.0025 | +0.137 |
| 15 | Thebe | 2.2205 | 2.0835 | -0.1370 | -6.170 |
| 1 | Io | 4.2482 | 4.1670 | -0.0812 | -1.911 |
| 2 | Europa | 6.7614 | 6.945 | +0.1836 | +2.7150 |
| 3 | Ganymede | 10.7811 | 11. 1120 | +0.3309 | +3.0690 |
| 4 | Callisto | 18.9919 | 18.5200 | -0.4719 | -2.4850 |
| 13 | Leda | 111.3809 | 111.1200 | -0.2609 | -0.2340 |
| 6 | Himalia | 114.9508 | 114.8240 | -0.1268 | -0.1100 |
| 10 | Lysithia | 117.0927 | 116.6760 | -0.4167 | -0.3560 |
| 7 | Elar | 117.8067 | 117.6020 | -0.2047 | -0.1740 |
| 2 | Ananke | 207.7682 | 207.4200 | -0.3482 | -0.1680 |
| 11 | Carme | 224.1897 | 222.2400 | -1.9497 | -0.8700 |
| 8 | Pasiphae | 233.4715 | 233.3500 | -0.1215 | -0.0520 |
| 9 | Sinope | 237.7553 | 237.9800 | +0.2247 | +0.0950 |
* Ref. Snow, T.P., The Dynamic Universe: An Introduction to
Astronomy, West Publishing Company, 2nd Edn., (1985), P 210
Percentage deviation= (Computed distance-Observed distance ) /Observed distance ×100
TABLE-5 |
|||||
PERCENTAGE DEVIATION IN THE PREDICTED DISTANCES OF THE SATELLITES OF SATURN
|
|||||
| No | Name | Observed distance * x 105 km | Computed distance x 105 km | Difference x 105 km | Percentage deviation |
| 17 | Atlas | 1.3767 | 1.3880 | + 0.0113 | + 0.821 |
| 16 | 1980 S 27 | 1.3936 | 1.4027 | – 0.0090 | – 0.653 |
| 15 | 1980 S 26 | 1.4172 | 1.4175 | + 0.0003 | + 0.021 |
| 10 | Janus | 1.5143 | 1.5356 | + 0.0213 | + 1.406 |
| 11 | Epimetheus | 1.5143 | 1.5356 | + 0.0213 | + 1.406 |
| 1 | Mimas | 1.8551 | 1.8605 | + 0.0054 | + 0.291 |
| 2 | Enceladus | 2.3806 | 2.3625 | – 0.0181 | – 0.760 |
| 13 | Telesto | 2.9465 | 2.8350 | – 0.1115 | – 3.784 |
| 14 | Calypso | 2.9465 | 2.8350 | – 0.1115 | – 3.784 |
| 3 | Tethys | 2.9465 | 2.8350 | – 0.1115 | – 3.874 |
| No name I | 3.3001 | 3.3075 | + 0.0074 | + 0.224 | |
| 4 | Dione | 3.7742 | 3.7671 | – 0.0071 | – 0.188 |
| 12 | 1980 S 6 | 3.7809 | 3.7689 | – 0.0120 | – 0.317 |
| No name II | 3.7827 | 3.7726 | – 0.0101 | – 0.267 | |
| No name III | 4.6997 | 4.7250 | + 0.0253 | + 0.538 | |
| 5 | Rhea | 5.2710 | 5.1975 | – 0.0735 | – 1.394 |
| 6 | Tita | 12.2168 | 11.3400 | – 0.8768 | – 7.177 |
| 7 | Hyperion | 14.8110 | 14.8840 | + 0.0730 | + 0.493 |
| 8 | Iapetus | 35.6068 | 34.0200 | – 1.5868 | – 4.455 |
| 9 | Phoebe | 129.5285 | 128.5200 | – 1.0085 | – 0.779 |
* Ref. :Snow, T.P., The Dynamic Universe: An Introduction to Astronomy,
West Publishing Co., 2nd. Ed., (1985) P 225, 231, (O-Outer; I – Inner)
TABLE-6 |
||||
PERCENTAGE DEVIATION IN THE PREDICTED DISTANCES OF THE RINGS OF SATURN |
||||
| Name | Observed distance * x 105 km |
Computed distance x 105 km |
Difference x 105 km |
Percentage deviation
|
|
I Ring D O |
0.6697 |
0.7088 |
……. |
…….. |
|
I Ring C O |
0.7439 |
0.8269 |
……. |
…….. |
|
I Ring B O |
0.9194 1.1740 |
0.9450 |
……. |
…….. |
|
I Ring A O |
1.2193 1.3665 |
1.1812 ……. |
……. ……. |
…….. ……. |
|
I Ring F O |
1.4033 |
1.4175 |
+0.0142 |
-2.102 |
|
I Ring G O |
1.6892 |
1.6537 |
-0.0355 ……. |
-2.102 …….. |
|
I Ring E O |
4.8264 |
3.7800 |
……. |
…….. |
* Ref. :Snow, T.P., The Dynamic Universe: An Introduction to Astronomy,
West Publishing Co., 2nd. Ed., (1985) P 225, 231, (O-Outer; I – Inner)
TABLE-7 |
|||||
PERCENTAGE DEVIATION IN THE PREDICTED DISTANCES OF THE SATELLITES AND RINGS OF URANUS
|
|||||
| No | Name | Observed distance * x 105 km |
Computed distance x 105 km |
Difference x 105 km | Percentage deviation |
| 1 | 1986 U2R | 3.70 – 3.95 | 3.7632 | 0.0000 | 0.000 |
| 2 | 6 Ring | 4.185 | 4.1664 | – 0.0186 | – 0.444 |
| 3 | 5 Ring | 4.224 | 4.2336 | + 0.0096 | +0.227 |
| 4 | 4 Ring | 4.258 | 4.2672 | + 0.0092 | +0.216 |
| 5 | 4.473 | 4.4352 | – 0.0378 | -0.845 | |
| 6 | 4.567 | 4.5696 | + 0.0026 | +0.057 | |
| 7 | 4.718 | 4.7040 | – 0.0140 | -0.297 | |
| 8 | 4.763 | 4.7712 | + 0.0082 | -0.172 | |
| 9 | 4.831 | 4.8384 | + 0.0074 | +0.153 | |
| 10 | 1986 UIR | 5.004 | 4.9728 | – 0.0312 | – 0.624 |
| 11 | 5.116 | 5.1072 | – 0.0088 | – 0.172 | |
| 12 | 1986 U7 | 4.970 | 4.9728 | – 0.0312 | – 0.624 |
| 13 | 1986 U8 | 5.380 | 5.3764 | – 0.0036 | – 0.067 |
| 14 | 1986 U9 | 5.920 | 5.9136 | – 0.0064 | – 0.108 |
| 15 | 1986 U3 | 6.180 | 6.1824 | + 0.0024 | +0.039 |
| 16 | 1986 U6 | 6.270 | 6.3168 | + 0.0468 | +0.746 |
| 17 | 1986 U2 | 6.460 | 6.4176 | – 0.0424 | – 0.656 |
| 18 | 1986 U1 | 6.610 | 6.5856 | – 0.0244 | – 0.369 |
| 19 | 1986 U4 | 6.990 | 6.9888 | – 0.0012 | – 0.017 |
| 20 | 1986 U5 | 7.530 | 7.5264 | – 0.0036 | – 0.048 |
| 21 | 1985 U1 | 8.600 | 8.6016 | + 0.0016 | +0.019 |
| 22 | Miranda | 12.990 | 12.9024 | – 0.0876 | -0.674 |
| 23 | Ariel | 19.090 | 19.3536 | + 0.2636 | +1.381 |
| 24 | Umbriel | 26.600 | 26.3424 | – 0.2576 | – 0.970 |
| 25 | Titania | 43.630 | 43.0080 | – 0.6220 | -1.426 |
| 26 | Oberon | 58.340 | 58.0606 | – 0.2794 | -0.479 |
* Ref. Stone, E.C. and Miner, E.D. “The Voyager 2 Encounter with the Uranian System” SCIENCE, Vol. 223, 4 July 1986, p 41.
Percentage deviation = (Computed distance-Observed distance) /Observed distance x 100
may have secondary effects in modulating the shell, sub-shell structure, formed primarily by the central gravitating body. Though the anticipated undulated gravity with humps provides large number of possible locations for placement of stable orbital bodies but the actual occurrences depends on the cosmic history. This makes many shells and sub-shells to remain vacant without an orbital body being present in it.
Conclusion
The shell, sub-shell features in the extranuclear space surrounding a celestial body as anticipated here with definite correlation remarkably reveals the discrete nature of orbits for celestial body systems. The new model exactly fits for the planets of the sun and the satellites of respective planets. The new model also reduces the gap between the atomic systems and the celestial body systems by identifying discreteness in the orbits of celestial bodies in solar system. A detailed study of the nature of gravitational interaction vis a vis this newly observed discrete orbit phenomenon will provide adequate knowledge for the formation of energy wells and might as well speak for the cause of gravity.
This article is a part of the original work published in the book “Planetary electrodynamics-1”, Volume-1 of the series “Dynamics of universe; interplay of matter, space and charge”, 1998 by the same author.
References
1. Moore, P., ‘Astronomy’, Oldbourne Book Co. Ltd., London, 2nd Rev. Edn. 1964, p.98
2. Moore, P., ‘The A-Z of Astronomy‘, William Collins Son Co. Ltd., 3rd Edition, Glasgow, 1978.
3. `Hand Book of Chemistry and Physics’, CRC Press, 60th Edn. 1979-80.
