INSTITUTE OF PHILOSOPHY OF NATURE
Abstract
Angular momentum is crucial in analysing the motion of orbital bodies. It explains how forces and torques affect the rotation of objects. In integral systems with torsional integrity, angular momentum is conserved provided there is no exchange of angular momentum with external bodies. For example, ice skaters pull in their arms to spin more. Angular momentum principles are used in the design of rotating machinery, such as turbines, flywheels and gyroscopes, etc. ensuring stability and performance. Athletes optimize their movements for better performance in gymnastics, diving, and figure skating. Angular momentum is essential in controlling the motion of robotic arms and other mechanisms involving rotation. Hence, conservation of angular momentum is a reality beyond doubt for systems having torsional linkage of component systems. But undue extrapolation of conservation of angular momentum in systems where it is not feasible leads to violation of the principle of conservation of angular momentum. An orbital body in the solar system does not have a torque transfer link with the central body hence the angular momentum is always zero with respect to the central body irrespective of different orbital distance and orbital velocity. The fluid dynamics model of the solar system does not require the angular momentum to justify the change of velocity at different orbital distances (Kepler’s Law). The wheeling extra nuclear space structure of the central body has different spatial tangential velocity given by v= √(GM/ R) and the same is discussed by this author in article-3, issue-3, volume-2 of this journal. The orbital body under equal and opposite centripetal force (gravity) and centrifugal force floats in the spinning extra nuclear space fluid of the central body and acquires the velocity of its adjacent space fluid. We, however, unknowingly ignore the reality by ignoring the role of space fluid and try to correlate the variation of orbital velocity with orbital distance from hypothetical conservation of angular momentum which is not feasible for orbital bodies without having a torque transfer link.
Key Words: Orbital bodies, Kepler’s Law, Angular momentum, Fluid dynamic model, Charge velocity, Extra nuclear space structure, Centripetal force, Centrifugal force.
Discussion
If a celestial body passes nearby another celestial body the moving celestial body cannot produce a torsional effect on the central body without a torque transfer link hence it has no scope in exchanging angular momentum between the moving celestial body and the stationary celestial body. The consideration of angular momentum of the orbital celestial body about the central celestial body without a torque transfer link is purely a hypothetical case. Gravitational attraction of the central body on an orbital celestial body acts along the line joining the bodies. Therefore, the gravity of the central body cannot produce tangential acceleration of the orbital body which is at right angles to radial acceleration. We make use of this phenomenon in solving problems of projectiles on the surface of the earth. For example, a bullet fired horizontally (tangential to the earth) from the top of a tall building maintains its constant horizontal velocity without acceleration. On the other hand, the bullet accelerates in the vertical direction due to gravity of the earth. The above consideration is used for calculating the horizontal range of the bullet. We don’t consider conservation of angular momentum about the center of the earth. If we consider conservation of angular momentum then the horizontal velocity of the bullet would increase with decrease of height of the bullet in its flight and introduce error in the evaluation of horizontal range of the bullet. An orbital celestial body does not have intelligence nor have memory of its orbit to retrace the path. At any instant, the orbital body has only tangential velocity, gravitational attraction and centrifugal force. Hence, the path traced by the orbital body can be determined only from its prevailing velocity and acceleration due to gravity and centrifugal force.
An orbital body in a circular path experiences both gravity (centripetal force) and centrifugal force. The orbital body in circular motion experiences a radially outward pull to restore its position along the path of inertial motion which produces the centrifugal force. Hence an orbital celestial body at certain orbital distance and tangential velocity, can have its centrifugal force equal and opposite to gravity where the orbital body would orbit in a circular path by the whirling space fluid of the central body without causing centripetal or centrifugal acceleration. However, if somehow the orbital body is displaced towards the central body, gravity would predominate over the centrifugal force and the predominance would go on increasing till it meets the central body. On the other hand, if the orbital body is displaced outwardly the centrifugal force would predominate and take the body away from the circular orbit overcoming gravity of the central body. But this doesn’t happen in reality. Observation shows that, tangential velocity increases when the orbital body comes closer to the central body and decreases when the orbital body goes away from the central body. It is, as if, conservation of angular momentum plays a part in the above phenomenon. The fact that gravitational force is at right angle to tangential velocity, the centripetal acceleration due to gravity cannot increase the tangential velocity. Therefore, increase of tangential velocity when the body is accelerated toward the central body and decrease of tangential velocity when the body is accelerated outwardly need justification from proper dynamics. This author has shown how the whirling physical space fluid of the extra-nuclear structure of the central celestial body reorients the velocity gain by radial acceleration in tangential direction that justifies Kepler’s observational law [1]. In the existing concept, angular momentum quantifies “rotational influence” without requiring a torsional link because it is a purely kinematic and dynamic property that arises from the relationship between the motion of the mass, its position and the reference axis. The concept of angular momentum has no meaning without a torsional link; therefore, the concept is purely hypothetical. Even if the mathematical quantification of rotational influence is giving results by assuming conservation of angular momentum, it is not enough to accept the same as reality since the very concept of angular momentum is lost without a torsional link. Then it becomes obvious that some unknown mechanism is operating in orbital dynamics that justifies the correlation between tangential velocity and radial distance. If the reality remains hidden to us then we can only justify the change of tangential velocity of an orbital body with orbital distance by making unrealistic hypotheses such as conservation of angular momentum. One can realize the significance of the above statement from the following example.
Our early concept was that the sun goes around the earth which gave rise to mathematical quantification of the length of the day. But now we know the reality that the earth rotates and revolves around the sun and the new knowledge also produces the same result on the length of the day. Any concept yielding result cannot be considered a reality if the concept is not feasible. A real phenomenon not only yields results but also has to be feasible.
The concept of conservation of angular momentum of orbital celestial bodies yields results but angular momentum of an orbital body without a torque transfer link is not feasible hence not a reality. Therefore, it is rational to look for the exact dynamics that predicts the orbital velocity in a realistic manner without involving conservation of angular momentum. If angular momentum does not change in the orbital dynamics then it is, as good as, not having a role in the dynamics. The new concept of fluid dynamics in the solar system is realistic and explains the motion of orbital bodies and makes the angular momentum redundant. The hypothetical concept of angular momentum without a rigid torsional link is not a valid consideration. This may be realized from the following example. Consider a nucleus body of mass ‘M’ and an orbital body of mass ‘m’. Both masses M and m are connected by flexible thread of length ‘l’ that can only execute the pull of ‘M’ on ‘m’ but cannot produce a torque on m about M. Hence, in the absence of torque transmission link, the tangential velocity of orbital body cannot be changed by variation of gravitational pull from central body. Hence, the variation of tangential velocity by conservation of angular momentum is purely hypothetical and not applicable for orbital dynamics. The increase of orbital velocity of the celestial body with decrease of orbital distance and decrease of orbital velocity with increase of orbital distance is derivable from realistic fluid dynamics [2]. In the lack of perception of fluid dynamics, the above phenomenon is attributed to hypothetical- ‘conservation of angular momentum’. However, the very feasibility of conservation of angular momentum is questionable.
An orbital body at any instance has a position in the orbit and orbital velocity which is tangential to the orbit. The present consideration of conservation of angular momentum about the central body is only hypothetical in the absence of a torque transfer link which is an essential requirement for angular momentum. The gravitational acceleration is radially inward therefore having a little influence on tangential acceleration. Further, an orbital body is a non-living thing hence it cannot remember its orbital path like a living being. Thus, for the orbital body, the instantaneous dynamic parameters (velocity) and the external forces (gravity and centrifugal force) make its next move progressively generating its path which may lead to a closed orbit (circle or ellipse) or spiral-in/spiral-out the central body. The nature of gravity and centrifugal force cannot provide stability to orbital bodies without an auto adjustable nature of force. The author has discussed a new celestial charge interaction elsewhere [3]. The negative celestial charge of an orbital body (say, the earth) is reduced in its movement towards the sun by receiving more quantity of positively charged solar radiation (photons) carrying photonic charge due to greater solid angle subtended by the planet (Fig.1).
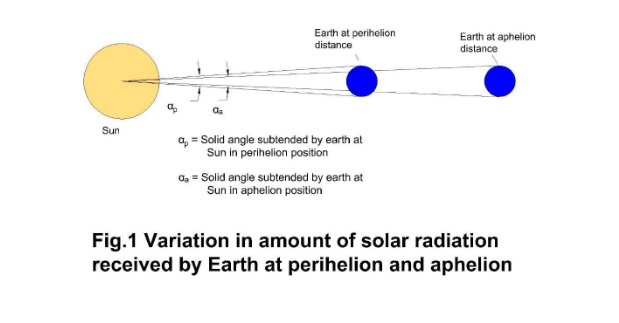
Thus, the net centripetal force (gravity and celestial charge attraction) reduces and at some point (perihelion) the centrifugal force dominates where the inward acceleration reverses to outward direction and the orbital body approaches the metastable circular orbit where the centripetal force becomes equal to centrifugal force. The orbital body, however, continues its outward motion beyond the circular orbit due to inertia of motion. At aphelion the solid angle is smaller and the negative charge of the orbital body increases where the net centripetal force supersedes the centrifugal force thereby the acceleration of the orbital body reverses to inward direction and the orbital body approaches the circular orbit. The cycle repeats, making radial oscillation of the orbital body over and above its orbital motion in circular orbit. The resultant of above two motions forms the stable elliptical orbit of the orbital body. It is for this reason the orbits of all orbital bodies are elliptical and the ellipse are close to the circle. The whirling extra-nuclear space structure of the central celestial body plays a great role in the stability of orbital bodies. The fluid dynamics in the solar system does not require the consideration of hypothetical conservation of angular momentum.
Conclusion
Conservation of angular momentum of orbital bodies has been greatly vindicated and well established in orbital dynamics even though it lacks reality. The consideration of angular momentum for orbital bodies is hypothetical and deviates from reality. The newly proposed fluid dynamics of the solar system is realistic and explains Kepler’s law. Thus, the present consideration only proxies the reality.
Reference
- https://philosophyofnature.org.in/new-findings-on-placement-of-orbital-bodies-and-new-characterization-of-motion-of-orbital-celestial-bodies.
- https://philosophyofnature.org.in/direction-of-revolution-and-rotation-of-orbital-bodies.
- https://philosophyofnature.org.in/electric-and-non-electric-charges-and-their-inter-conversion.
